题目内容
8.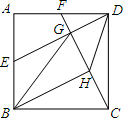 如图,在正方形ABCD中,点E是AB中点,点F是AD上一点,且DE=CF,ED、FC交于点G,连接BG,BH平分∠GBC交FC于H,连接DH.
如图,在正方形ABCD中,点E是AB中点,点F是AD上一点,且DE=CF,ED、FC交于点G,连接BG,BH平分∠GBC交FC于H,连接DH.(1)若DE=10,求线段AB的长;
(2)求证:BG=BC;
(3)求证:DE-HG=EG.
分析 (1)设AE=x,则AD=2x,在直角三角形AED中利用勾股定理即可求出x的值,进而求出AB的长;
(2)利用已知得出B、C、G、E四点共圆,得出BG=BC,
(3)证得BH是GC的中垂线,再利用△BHC≌△CGD,得出GH=DG即可证明DE-HG=EG.
解答 (1)解:设AE=x,则AD=2x,
∵四边形ABCD是正方形,
∴∠A=90°,
∴x2+(2x)2=102,
∴x=2$\sqrt{5}$,
∴AB=2AE=4$\sqrt{5}$;
(2)证明:在正方形ABCD中,
易证RT△CDF≌RT△DAE,
∴∠FCD=∠ADE,
∴∠GDC+∠DCF=90°,
∴∠DGC=∠CGE=90°,
∴∠EGC=∠EBC=90°,
∴∠EGC+∠EBC=180°,
∴B、C、G、E四点共圆,
∠AED=∠BCG,
连EC,
∴∠BGC=∠BEC,
∵BE=EA,BC=AD,
∴RT△BCE≌RT△ADE,
∴∠AED=∠BEC,
∴∠BGC=∠AED,
∴∠BGC=∠BCG,
∴BG=BC;
(3)证明:∵BH平分∠GBC,
∴BH是GC的中垂线,
∴GH=HC,
∴GH=DG,
∴△DGH是等腰直角三角形,
即:DE-HG=EG.
点评 此题主要考查了全等三角形的判定与四点共圆的性质与判定,根据已知得出B、C、G、E四点共圆,以及BG是GC的中垂线是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知a、b、c三个数在数轴上对应点的位置如图所示,下列判断错误的有( )

①a<c<b②-a<b③a+b>0④c-a<0.

①a<c<b②-a<b③a+b>0④c-a<0.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.若整数a使关于x的不等式组$\left\{\begin{array}{l}{\frac{1}{2}(x-3)+\frac{x}{2}≥3}\\{\frac{a-3x}{3}>0}\end{array}$无解,且使关于x的分式方程 $\frac{ax}{x-3}+\frac{3}{3-x}$=-2有整数解,那么所有满足条件的a值的和是( )
| A. | -20 | B. | -19 | C. | -15 | D. | -13 |
20.已知?ABCD的周长为32,AB=6,则BC等于( )
| A. | 10 | B. | 12 | C. | 24 | D. | 28 |
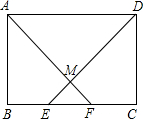 如图,在矩形ABCD中,点E.点F在BC边上,且BE=CF,AF,DE交于点M.求证:
如图,在矩形ABCD中,点E.点F在BC边上,且BE=CF,AF,DE交于点M.求证: