题目内容
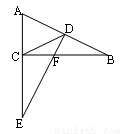
（8分）如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，若∠PAB=40°，求∠P的度数．
100°
【解析】
试题分析：首先连接OB，根据切线的性质得到∠PAO=∠PBO，根据OA=OB得到∠OAB=∠OBA，从而说明∠PAB=∠PBA，最后根据△PAB的内角和定理求出∠P的度数．
试题解析：连接OB，∵PA和PB为切线 ∴∠PAO=∠PBO=90° ∵OA=OB ∴∠OAB=∠OBA
∴∠PAO－∠OAB=∠PBO－∠OBA ∴∠PBA=∠PAB=40° ∴∠P=180°－（∠PAB+∠PBA）=100°．
考点：切线的性质、等腰三角形的性质
练习册系列答案
优学名师名题系列答案
相关题目
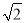，⊙O的半径为1，P是AB边上的动点，过点P作⊙O的切线PQ，切点为Q，则切线长PQ的最小值为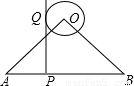 
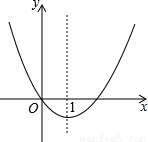
x2＋bx＋c的图象经过B、C两点．现将一把直尺放置在直角坐标系中，使直尺的边A'D'∥y轴且经过点B，直尺沿x轴正方向平移，当A'D'与y轴重合时运动停止．
时，线段PA、PB、PC之间的数量关系．请直接写出结论，并指出相应的点P与抛物线的位置关系．
=x的解是 ．
