题目内容
11. 在菱形ABCD中,AE⊥DC于E,EC=1,cosB=$\frac{5}{13}$,求这个菱形的面积.
在菱形ABCD中,AE⊥DC于E,EC=1,cosB=$\frac{5}{13}$,求这个菱形的面积.
分析 由菱形的性质得出AD=DC,∠D=∠B,设菱形的边长AD=DC=x,则DE=x-1.由三角函数得出方程,解方程求出菱形的边长,再由三角函数求出AE,即可得出结果.
解答 解:∵四边形ABCD是菱形,
∴AD=DC,∠D=∠B,
设菱形的边长AD=DC=x,
则DE=x-1.
∵cosD=cosB=$\frac{5}{13}$,
∴$\frac{DE}{AD}$=$\frac{x-1}{x}$=$\frac{5}{13}$,解得:x=$\frac{13}{8}$,
∴DE=$\frac{5}{8}$,
∵cosD=$\frac{5}{13}$,
∴sinD=$\frac{AE}{AD}$=$\frac{12}{13}$,
∴AE=$\frac{12}{13}$×$\frac{13}{8}$=$\frac{3}{2}$.
故:S菱形=DC×AE=$\frac{13}{8}$×$\frac{3}{2}$=$\frac{39}{16}$.
点评 本题考查了三角函数、菱形的性质、菱形面积的计算方法;熟练掌握菱形的性质,由三角函数求出边长和高是解决问题的关键.

练习册系列答案
相关题目
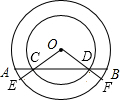 如图,以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D,OC、OD的延长线交大圆于E、F.求证:$\widehat{AE}$=$\widehat{BF}$.
如图,以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D,OC、OD的延长线交大圆于E、F.求证:$\widehat{AE}$=$\widehat{BF}$. 如图,是由一些大小相同的小正方体搭成的简单几何体.
如图,是由一些大小相同的小正方体搭成的简单几何体. 从点P向⊙O引两条切线PA,PB,切点为A,B,AC为弦,BC为⊙O直径,若∠P=60°,PB=2cm,求:
从点P向⊙O引两条切线PA,PB,切点为A,B,AC为弦,BC为⊙O直径,若∠P=60°,PB=2cm,求:

 如图,桃花源管理处为了方便游客,决定在一条水平宽为100m,高为100m的山坡上铺设石板路,设AB是坡面,每块石板宽25cm(石板的厚度忽略不计),铺设方法如图所示,需购买这种石板多少块?
如图,桃花源管理处为了方便游客,决定在一条水平宽为100m,高为100m的山坡上铺设石板路,设AB是坡面,每块石板宽25cm(石板的厚度忽略不计),铺设方法如图所示,需购买这种石板多少块?