题目内容
1.有一次考试共20题,每做对一题得8分,做错一题扣5分,不做得0分,考试时小张得13分,则小张没有做对7道.分析 假设该生做对x个题,做错y个题,没做的是z个题.根据一次考试共需做20个小题得到方程x+y+z=20;根据做对一个得8分,做错一个减5分,不做的得0分.某学生共得13分得方程8x-5y=13,然后解不定方程后讨论即可得出答案.
解答 解:设该生做对x个题,做错y个题,没做的是z个题.
根据题意列方程组,
$\left\{\begin{array}{l}{x+y+z=20①}\\{8x-5y=13②}\end{array}\right.$,
由①×5+②得:13x+5z=113③,
根据③式可知,5z的个位数必是0、5,所以13x的个位数必是3、8,且1≤x≤8,
①当x=1时,z=20,不合题意舍去;
②当x=2时,不合题意舍去;
③当x=3时,不合题意舍去;
④当x=4时,不合题意舍去;
⑤当x=5时,不合题意舍去;
⑥当x=6时,z=7,y=7;
⑦当x=7时,不合题意舍去;
⑧当x=8时,不合题意舍去.
故答案为7.
点评 本题考查了三元一次方程的应用,解决本题的关键是尽量缩小对于未知数的讨论范围.根据方程13x+5z=113得知5z的个位数必是0、5,所以13x的个位数必是3、8,且1≤x≤8,难度较大.

练习册系列答案
相关题目
16.下列各组数是勾股数的是( )
| A. | 2,3,4 | B. | 4,5,6 | C. | 3.6,4,8.6 | D. | 9,40,41 |
13.下列事件为必然事件的是( )
| A. | 任意买一张电影票,座位号是偶数 | |
| B. | 打开电视机,CCTV第一套节目正在播放天气预报 | |
| C. | 从一个之装有红色小球的把它们袋中,任意摸出一球是红球 | |
| D. | 经过某一有交通信号灯的路口,恰好遇到红灯 |
11.某市“五一”期间13条高速公路免费放行247万辆车次,免费余额预计达到4960万元,将4960万元用科学记数法表示为( )元.
| A. | 4.96×105 | B. | 4.96×104 | C. | 4.96×106 | D. | 4.96×107 |
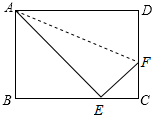 如图,折叠矩形ABCD的一边AD使点D落在BC边上的E处,已知折痕AF=10cm,且tan∠FEC=$\frac{3}{4}$.
如图,折叠矩形ABCD的一边AD使点D落在BC边上的E处,已知折痕AF=10cm,且tan∠FEC=$\frac{3}{4}$.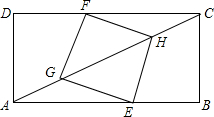 如图,矩形ABD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形.
如图,矩形ABD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形. 如图,点P是△ABC内一点,连接BP,并延长交AC于点D.
如图,点P是△ABC内一点,连接BP,并延长交AC于点D.
 如图,∠B=80°,∠C=50°,AD是△ABC的高,AE是∠CAB的平分线,求∠DAE.
如图,∠B=80°,∠C=50°,AD是△ABC的高,AE是∠CAB的平分线,求∠DAE.