题目内容
15. 如图,△ABC的三个顶点在⊙0上,D为$\widehat{BC}$中点,连接AD,0D,∠B=80°,∠C=40°.求:∠ODA的度数.
如图,△ABC的三个顶点在⊙0上,D为$\widehat{BC}$中点,连接AD,0D,∠B=80°,∠C=40°.求:∠ODA的度数.
分析 根据三角形的内角和得到∠BAC=180°-∠B-∠C=60°,根据已知条件得到∠BAD=∠CAD=30°,OD⊥BC,求得∠EFD=90°,根据对顶角和三角形的内角和即可得到结论.
解答  解:如图,∵∠B=80°,∠C=40°,
解:如图,∵∠B=80°,∠C=40°,
∴∠BAC=180°-∠B-∠C=60°,
∵D为$\widehat{BC}$中点,
∴∠BAD=∠CAD=30°,OD⊥BC,
∴∠EFD=90°,
∵∠FED=∠AEB=180°-∠B-∠BAE=70°,
∴∠ODA=20°.
点评 本题考查了圆周角定理,垂径定理,三角形的内角和,熟练掌握圆周角定理是解题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
7.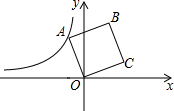 如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值是( )
如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值是( )
 如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值是( )
如图,在平面直角坐标系中,正方形ABCD的顶点O在坐标原点,点B的坐标为(1,4),点A在第二象限,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值是( )| A. | -2 | B. | -4 | C. | -$\frac{15}{4}$ | D. | $\frac{15}{4}$ |
 如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中小正方形顶点A,B围成的正方体上的距离是1.
如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中小正方形顶点A,B围成的正方体上的距离是1.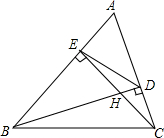 如图,△ABC中,高BD、CE相交于点H,求证:
如图,△ABC中,高BD、CE相交于点H,求证: