题目内容
18.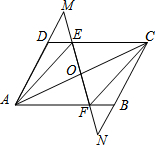 如图,平行四边形ABCD中,EF过对角线AC的中点O,且EF⊥AC交CD于E,交AB于F,分别交AD、CB的延长线于M、N.
如图,平行四边形ABCD中,EF过对角线AC的中点O,且EF⊥AC交CD于E,交AB于F,分别交AD、CB的延长线于M、N.(1)证明:DM=BN;
(2)连接AE、CF,判断四边形AECF的形状,并说明理由.
分析 (1)由平行四边形的性质得出AD=CB,AM∥CN,证出∠M=∠N,再由AO=CO,根据AAS证明△AOM≌△CON,得出AM=CN,即可得出结论;
(2)由ASA证明△AOF≌△COE,得出OF=OE,证出四边形AECF是平行四边形,再由对角线互相垂直,即可得出四边形AECF是菱形.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,AM∥CN,AB∥CD,
∴∠M=∠N,
∵EF垂直平分AC,
∴∠AOM=∠CON=90°,AO=CO,
在△AOM和△CON中,
$\left\{\begin{array}{l}{∠M=∠N}&{\;}\\{∠AOM=∠CON}&{\;}\\{AO=CO}&{\;}\end{array}\right.$,
∴△AOM≌△CON(AAS),
∴AM=CN,
∵AM-AD=CN-CB,
∴DM=BN.
(2)解:四边形AECF是菱形;理由如下:
∵AB∥CD,
∴∠ACE=∠CAF,
∵EF垂直平分AC,
∴∠COE=∠AOF=90°,AO=CO,
在△AOF和△COE中,
$\left\{\begin{array}{l}{∠AOF=∠COE}&{\;}\\{AO=CO}&{\;}\\{∠ACE=∠CAF}&{\;}\end{array}\right.$,
∴△AOF≌△COE(AAS),
∴OF=OE,
∴四边形AECF是平行四边形,
∵EF⊥AC,
∴四边形AECF是菱形.
点评 本题考查了平行四边形的性质与判定、全等三角形的判定与性质、菱形的判定;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.某厂共有120名生产工人,每个工人每天可生产螺栓50个或螺母20个,已知一个螺栓与两个螺母配成一套,设每天安排x名工人生产螺栓,y名工人生产螺母,才能使每天生产出来的产品配成最多套.则所列的方程组是( )
| A. | $\left\{\begin{array}{l}{x+y=120}\\{50x=20y×2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=120}\\{50x=20y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{50x+20y=120}\\{50x×2=20y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=120}\\{50x×2=20y}\end{array}\right.$ |
10.一次函数y=-2x-1的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,数轴的单位长度为1,如果R表示的数是-1,则数轴上表示相反数的两点是P,Q.
如图,数轴的单位长度为1,如果R表示的数是-1,则数轴上表示相反数的两点是P,Q.