题目内容
8.A、B是两个多项式,其中A-B=a2+ab+b2,且B=$\frac{1}{2}$ab-3b2.(1)求多项式A.(用含a、b的代数式表示)
(2)若|a-2|+(b+3)2=0,求这个多项式A的值.
分析 (1)把B代入A-B中,去括号合并确定出A即可;
(2)利用非负数的性质求出a与b的值,代入计算即可求出A的值.
解答 解:(1)由题意得:A-($\frac{1}{2}$ab-3b2)=a2+ab+b2,
整理得:A=$\frac{1}{2}$ab-3b2+a2+ab+b2=a2+$\frac{3}{2}$ab-2b2;
(2)由|a-2|+(b+3)2=0,得到$\left\{\begin{array}{l}{a-2=0}\\{b+3=0}\end{array}\right.$,
解得:a=2,b=-3,
代入得:A=4-9-18=-23.
点评 此题考查了整式的加减,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.下列随机事件的概率,既可以用列举法求得,又可以用频率估计获得的是( )
| A. | 某种幼苗在一定条件下的移植成活率 | |
| B. | 某种柑橘在某运输过程中的损坏率 | |
| C. | 某运动员在某种条件下“射出9环以上”的概率 | |
| D. | 投掷一枚均匀的骰子,朝上一面为偶数的概率 |
17.某品牌LED电视机经过连续两次降价,每台售价由原来的4000元降到了2980元,设平均每次降价的百分率为x,则下列方程中正确的是( )
| A. | 4000(1+x)2=2980 | B. | 2980(1+x)2=4000 | C. | 2980(1-x)2=4000 | D. | 4000(1-x)2=2980 |
18.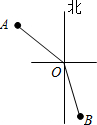 在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,则∠AOB的大小为( )
在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,则∠AOB的大小为( )
 在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,则∠AOB的大小为( )
在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,则∠AOB的大小为( )| A. | 69° | B. | 111° | C. | 159° | D. | 141° |
 一个几何体由几个大小相同的小正方体搭成,从上面看和从左面看如图所示,则搭成这个几何体的小正方体的个数是4个.
一个几何体由几个大小相同的小正方体搭成,从上面看和从左面看如图所示,则搭成这个几何体的小正方体的个数是4个.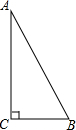 如图,在Rt△ABC中,AC=12mm,AB=13mm,在顶点A处有一只蚂蚁,以每秒4mm的速度沿AC方向爬行;在顶点B处有一只蜗牛,以每秒1mm的速度沿BC方向爬行.当它们同时出发爬行2秒后相距多少mm?
如图,在Rt△ABC中,AC=12mm,AB=13mm,在顶点A处有一只蚂蚁,以每秒4mm的速度沿AC方向爬行;在顶点B处有一只蜗牛,以每秒1mm的速度沿BC方向爬行.当它们同时出发爬行2秒后相距多少mm?