题目内容
3.边长为3的正六边形的面积为$\frac{27\sqrt{3}}{2}$.分析 根据题意画出图形,边长为3的正六边形可以分成六个边长为3的正三角形,计算出正六边形的面积即可.
解答 解:如图,连接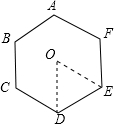 OD,OE,
OD,OE,
∵∠DOE=360°×$\frac{1}{6}$=60°,
又∵OD=OE,
∴∠ODE=∠OED=(180°-60°)÷2=60°,
∴三角形ODE为正三角形,
∴OD=OE=DE=3,
∴S△ODE=$\frac{1}{2}$OD•OE•sin60°=$\frac{1}{2}$×3×3×$\frac{\sqrt{3}}{2}$=$\frac{9\sqrt{3}}{4}$.
∴正六边形的面积=6×$\frac{9\sqrt{3}}{4}$=$\frac{27\sqrt{3}}{2}$.
故答案为:$\frac{27\sqrt{3}}{2}$.
点评 本题考查的是正多边形和圆,根据题意画出图形,构造出等边三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差S2:
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择甲.
| 甲 | 乙 | 丙 | 丁 | |
| 平均数x(cm) | 175 | 173 | 175 | 174 |
| 方差S2(cm2) | 3.5 | 3.5 | 12.5 | 15 |
15.下列调查中,最适合用普查方式的是( )
| A. | 了解某种节能灯的使用寿命 | B. | 了解10名运动员兴奋剂的使用情况 | ||
| C. | 了解我国农民的年人均收入情况 | D. | 了解某种炮弹的杀伤半径 |
 如图所示,每个小正方形的变成都是1厘米,现有一半径为1厘米的圆沿着图形内测运动,如果此圆作旋转(无滑动的滚动)运动,则它经过部分的面积是(34+$\frac{7}{2}π$)平方厘米.(答案保留π)
如图所示,每个小正方形的变成都是1厘米,现有一半径为1厘米的圆沿着图形内测运动,如果此圆作旋转(无滑动的滚动)运动,则它经过部分的面积是(34+$\frac{7}{2}π$)平方厘米.(答案保留π) 如图:线段AD=8cm,线段AC=BD=6cm,E、F分别是线段AB、CD的中点,求EF的长是多少?
如图:线段AD=8cm,线段AC=BD=6cm,E、F分别是线段AB、CD的中点,求EF的长是多少?
 如图,在⊙O中,AB是⊙O的直径,AB=8cm,C、D为弧AB的三等分点,M是AB上一动点,CM+DM的最小值是8cm.
如图,在⊙O中,AB是⊙O的直径,AB=8cm,C、D为弧AB的三等分点,M是AB上一动点,CM+DM的最小值是8cm.