题目内容
 如图,AB为⊙O的直径,CA、CD分别切⊙O于A、D,CO的延长线交⊙O于M,连BD、DM.
如图,AB为⊙O的直径,CA、CD分别切⊙O于A、D,CO的延长线交⊙O于M,连BD、DM.(1)求证:BD∥CM;
(2)若sinB=
| 4 |
| 5 |
考点:切线的性质
专题:
分析:(1)连结OD,如图,根据切线的性质得OA⊥AC,OD⊥CD,易证得Rt△OAC≌△Rt△ODC,则∠AOC=∠DOC,由圆周角定理得∠AOD=2∠OBD,而∠OBD=∠ODB,所以∠AOC=∠DOC=∠OBD=∠ODB,则可判断CM∥BD,
(2)由CM∥BD,所以∠BDM=∠M,而∠DOC=2∠M,则∠DOC=2∠BDM,即∠B=2∠BDM,从而求得∠AOC=2∠BDM,作OE平分∠AOC,交AC于E,作EF⊥OC,得出EF=AE,OA=OF,∠AOE=∠BDM,根据已知设AC=4x,OC=5x,则OA=3x,根据勾股定理求得AE和OA的关系,进而即可求得cos∠BDM.
(2)由CM∥BD,所以∠BDM=∠M,而∠DOC=2∠M,则∠DOC=2∠BDM,即∠B=2∠BDM,从而求得∠AOC=2∠BDM,作OE平分∠AOC,交AC于E,作EF⊥OC,得出EF=AE,OA=OF,∠AOE=∠BDM,根据已知设AC=4x,OC=5x,则OA=3x,根据勾股定理求得AE和OA的关系,进而即可求得cos∠BDM.
解答: 证明:(1)连结OD,如图,
证明:(1)连结OD,如图,
∵CA、CD分别与⊙O相切于A、D,
∴OA⊥AC,OD⊥CD,
在Rt△OAC和△Rt△ODC中,
,
∴Rt△OAC≌△Rt△ODC(HL),
∴∠AOC=∠DOC,
∴∠AOD=2∠AOC,
∵∠AOD=2∠OBD,
∴∠AOC=∠OBD,
∴BD∥CM.
(2)∵CM∥BD,
∴∠BDM=∠M,
∵OD=OB=OM,
∴∠ODM=∠OMD,∠ODB=∠B
∴∠DOC=2∠BDM,
∴∠B=2∠BDM.
∵∠AOC=∠B,
作OE平分∠AOC,交AC于E,作EF⊥OC,
∴EF=AE,OA=OF,∠AOE=∠BDM,
∴F在圆上,
设AE=EF=y,
∵sinB=
,
∴sin∠AOC=
=
,
∴设AC=4x,OC=5x,则OA=3x,
在RT△EFC中,EC=4x-y,CF=5x-3x=2x,
∴(4x-y)2=y2+(2x)2,
解得,y=
x,
∴OE=
=
=
x,
∴cos∠BDM=cos∠AOE=
=
=
.
 证明:(1)连结OD,如图,
证明:(1)连结OD,如图,∵CA、CD分别与⊙O相切于A、D,
∴OA⊥AC,OD⊥CD,
在Rt△OAC和△Rt△ODC中,
|
∴Rt△OAC≌△Rt△ODC(HL),
∴∠AOC=∠DOC,
∴∠AOD=2∠AOC,
∵∠AOD=2∠OBD,
∴∠AOC=∠OBD,
∴BD∥CM.
(2)∵CM∥BD,
∴∠BDM=∠M,
∵OD=OB=OM,
∴∠ODM=∠OMD,∠ODB=∠B
∴∠DOC=2∠BDM,
∴∠B=2∠BDM.
∵∠AOC=∠B,
作OE平分∠AOC,交AC于E,作EF⊥OC,
∴EF=AE,OA=OF,∠AOE=∠BDM,
∴F在圆上,
设AE=EF=y,
∵sinB=
| 4 |
| 5 |
∴sin∠AOC=
| AC |
| OC |
| 4 |
| 5 |
∴设AC=4x,OC=5x,则OA=3x,
在RT△EFC中,EC=4x-y,CF=5x-3x=2x,
∴(4x-y)2=y2+(2x)2,
解得,y=
| 3 |
| 2 |
∴OE=
| OA2+AE2 |
(3x)2+(
|
3
| ||
| 2 |
∴cos∠BDM=cos∠AOE=
| OA |
| OE |
| 3x | ||||
|
2
| ||
| 5 |
点评:本题考查了切线的性质,三角形全等的判定和性质,平行线的判定和性质,解直角三角形等,也考查了圆周角定理.作出辅助线构建直角三角形是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图是一个8×7的正方形网格图,且每个小正方形的边长为1.
如图是一个8×7的正方形网格图,且每个小正方形的边长为1.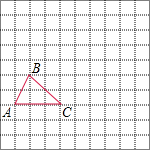 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).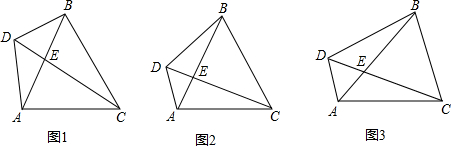
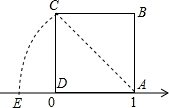 如图正方形ABCD一边在以点D为原点的数轴上,以点A为圆心,以AC长为半径画弧,且与数轴相交于点E,求数轴上的点E所对应的实数,并判断点E所对应的实数是有理数还是无理数?
如图正方形ABCD一边在以点D为原点的数轴上,以点A为圆心,以AC长为半径画弧,且与数轴相交于点E,求数轴上的点E所对应的实数,并判断点E所对应的实数是有理数还是无理数?