题目内容
10．解方程：（1）6x+2=4x-7
（2）$\frac{x+2}{3}$-$\frac{2x-1}{4}$=1．
分析 解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、系数化为1，据此求出每个方程的解各是多少即可．
解答 解：（1）移项，得6x-4x=-7-2
合并同类项，得2x=-9
系数化为1，得x=-4.5
（2）去分母，得4（x+2）-3（2x-1）=12
去括号，得-2x+11=12
移项，得-2x=12-11
合并同类项，得-2x=1
系数化为1，得x=-0.5
点评 此题主要考查了解一元一次方程的方法，要熟练掌握，解答此题的关键是要明确解一元一次方程的一般步骤：去分母、去括号、移项、合并同类项、系数化为1．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
20．
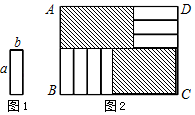如图1，将7张长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）
如图1，将7张长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（ ）| A． | a=b | B． | a=3b | C． | a=2b | D． | a=4b |
5．下列运算正确的是（ ）
| A． | -（-a+b）=a+b | B． | 3a3-3a2=a | C． | （x6）2=x8 | D． | 1÷（$\frac{2}{3}$）-1=$\frac{2}{3}$ |
15．若二次根式$\sqrt{3x-2}$无意义，则x的取值为（ ）
| A． | x≥$\frac{2}{3}$ | B． | x＞$\frac{2}{3}$ | C． | x＜$\frac{2}{3}$ | D． | x≤$\frac{2}{3}$ |
2．下列运算正确的是（ ）
| A． | 2a•5b=10ab | B． | （2x2）3=2x5 | C． | 3+$\sqrt{2}$=3$\sqrt{2}$ | D． | $\sqrt{6}$÷$\sqrt{3}$=2 |
20．如果以x=-5为方程的解构造一个一元一次方程，那么下列方程中不满足要求的是（ ）
| A． | x+5=0 | B． | x-7=-12 | C． | 2x+5=-5 | D． | -$\frac{x}{5}$=-1 |