��Ŀ����
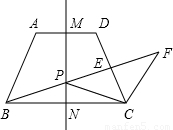
��֪��ͼ���ڵ�������ABCD�У�AD��BC��AB=CD��AD=3��BC=9��tan��ABC=| 4 | 3 |
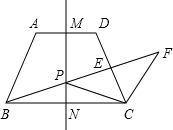 �ĶԳ��ᣬ��P���߶�MN��һ�����㣨����M��N�غϣ�������BP���߶�CD�ڵ�E������C��CF��AB������BP�ڵ�F��
�ĶԳ��ᣬ��P���߶�MN��һ�����㣨����M��N�غϣ�������BP���߶�CD�ڵ�E������C��CF��AB������BP�ڵ�F����1����֤��PC2=PE•PF��
��2����PN=x��CE=y���Խ���y��x֮��ĺ�����ϵʽ�������������
��3������PD���ڵ�P�˶������У������EFC�͡�PDC���ƣ����PN�ij���
��������1���������������ε��ж����������PEC�ס�PCF�����������������ε��������
=
��
��2������ƽ���ߵ����ʵó�
=
��
��3������������PN�ij���
| PC |
| PF |
| PE |
| PC |
��2������ƽ���ߵ����ʵó�
| PN |
| EG |
| BN |
| BG |
��3������������PN�ij���
����⣺��1����AD��BC��AB=CD��
���ABC=��DCB��
��ֱ��MN�����εĶԳ��ᣬ
��PB=PC��
���PBC=��PCB��
���ABP=��DCP��
��AB��CF
���ABP=��F
���F=��DCP��
�ߡ�EPC=��FPC��
���PEC�ס�PCF��
��PC2=PE•PF��
��2������E��EG��BC��G��
��tan��ABC=tan��DCB=
��
��EG=
y��GC=
y��
��������EG��MN��
��
=
����
=
��
��y=
��0��x��3����
��3��������PDC=��DCFʱ��PD��CF��
���F=��DPF��
��AB��CF��
���ABF=��DPF��
���MDP=��ABC��
��tan��MDP=tan��ABC=
��
��
=
��
��x=2��
������PDC=��FEC=��DEPʱ������P��PH��DE��AD���ӳ����ڵ�O��
��DH=EH=
��
���ODC=��DCB��
��DO=
=
•
��
�֡�
=
��
��x=
��
��Ϊ2���ڶ������ڣ����Ե�x=
��x=2ʱ����EFC�͡�PDC���ƣ�
���ABC=��DCB��
��ֱ��MN�����εĶԳ��ᣬ
��PB=PC��
���PBC=��PCB��
���ABP=��DCP��
��AB��CF
���ABP=��F
���F=��DCP��
�ߡ�EPC=��FPC��
���PEC�ס�PCF��
��PC2=PE•PF��
��2������E��EG��BC��G��

��tan��ABC=tan��DCB=
| 4 |
| 3 |
��EG=
| 4 |
| 5 |
| 3 |
| 5 |
��������EG��MN��
��
| PN |
| EG |
| BN |
| BG |
| x | ||
|
| 4.5 | ||
9-
|
��y=
| 15x |
| x+6 |
��3��������PDC=��DCFʱ��PD��CF��
���F=��DPF��
��AB��CF��
���ABF=��DPF��
���MDP=��ABC��
��tan��MDP=tan��ABC=
| 3 |
| 4 |
��
| 1.5 |
| 4-x |
| 3 |
| 4 |
��x=2��

������PDC=��FEC=��DEPʱ������P��PH��DE��AD���ӳ����ڵ�O��
��DH=EH=
| 5-y |
| 2 |
���ODC=��DCB��
��DO=
| DH |
| cos��ODH |
| 5-y |
| 2 |
| 5 |
| 3 |
�֡�
| MO |
| MP |
| 4 |
| 3 |
��x=
25��
| ||
| 16 |
��Ϊ2���ڶ������ڣ����Ե�x=
25��
| ||
| 16 |
��������Ҫ�������������ε��ж����������ʺ�ƽ���ߵ����ʣ�

��ϰ��ϵ�д�
 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�����Ŀ
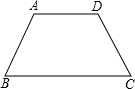 ��֪��ͼ���ڵ�������ABCD�У�AD��BC��
��֪��ͼ���ڵ�������ABCD�У�AD��BC��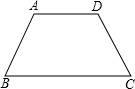 ��֪��ͼ���ڵ�������ABCD�У�AD��BC��
��֪��ͼ���ڵ�������ABCD�У�AD��BC�� ��֤����AC��BD��
��֤����AC��BD�� ��֤����AC��BD��
��֤����AC��BD��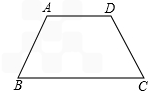
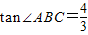 ��ֱ��MN�����εĶԳ��ᣬ��P���߶�MN��һ�����㣨����M��N�غϣ�������BP���߶�CD�ڵ�E������C��CF��AB������BP�ڵ�F��
��ֱ��MN�����εĶԳ��ᣬ��P���߶�MN��һ�����㣨����M��N�غϣ�������BP���߶�CD�ڵ�E������C��CF��AB������BP�ڵ�F��