Question

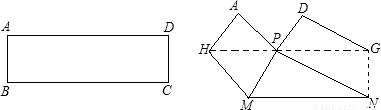
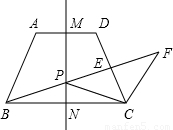
（2010•徐汇区二模）已知如图，在等腰梯形ABCD中，AD∥BC，AB=CD，AD=3，BC=9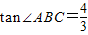，，直线MN是梯形的对称轴，点P是线段MN上一个动点（不与M、N重合），射线BP交线段CD于点E，过点C作CF∥AB交射线BP于点F．
（1）求证：PC²=PE•PF；
（2）设PN=x，CE=y，试建立y和x之间的函数关系式，并求出定义域；
（3）连接PD，在点P运动过程中，如果△EFC和△PDC相似，求出PN的长．

Answer 1

【答案】分析：（1）利用相似三角形的判定定理求出△PEC∽△PCF，再利用相似三角形的性质求出=；
（2）利用平行线的性质得出=；
（3）利用逆推求PN的长．
解答：解：（1）∵AD∥BC，AB=CD，
∴∠ABC=∠DCB，
∵直线MN是梯形的对称轴，
∴PB=PC．
∴∠PBC=∠PCB，
∴∠ABP=∠DCP，
∵AB∥CF
∴∠ABP=∠F
∴∠F=∠DCP．
∵∠EPC=∠FPC，
∴△PEC∽△PCF，
∴PC²=PE•PF；

（2）过点E作EG⊥BC于G．
∵，
∴．
由题意有EG∥MN，
∴，即，
∴y=（0＜x≤3）；

（3）（Ⅰ）当∠PDC=∠DCF时，PD∥CF，
∴∠F=∠DPF，
∵AB∥CF，
∴∠ABF=∠DPF，
∴∠MDP=∠ABC，
∵tan∠MDP=tan∠ABC=，
∴，
∴x=2．
（Ⅱ）当∠PDC=∠FEC=∠DEP时，过点P作PH⊥DE交AD的延长线于点O．
则．
∴∠ODC=∠DCB，
∴DO==，
又∵，
∴．
因为2都在定义域内，所以当x=或x=2时，△EFC和△PDC相似．
点评：主要考查相似三角形的判定定理及性质和平行线的性质．