题目内容
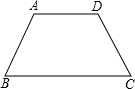 已知如图,在等腰梯形ABCD中,AD∥BC.
已知如图,在等腰梯形ABCD中,AD∥BC.(1)若AD=5,BC=11,梯形的高是4,求梯形的周长;
(2)若AD=3,BC=7,BD=5
| 2 |
分析:(1)作出BC边上的高,解直角三角形得出梯形各个边的长,进而可求周长.
(2)可设A,D在BC上的垂线的垂足分别是E,F.AC,BD交于O,通过解直角三角形可得△BFD为等腰直角三角形,进而可证AC⊥BD.
(2)可设A,D在BC上的垂线的垂足分别是E,F.AC,BD交于O,通过解直角三角形可得△BFD为等腰直角三角形,进而可证AC⊥BD.
解答: 解:(1)如图,过点A作AE⊥BC,
解:(1)如图,过点A作AE⊥BC,
∴AE=4,又AD=5,BC=11,∴BE=
(BC-AD)=3,
∴CD=AB=5,
∴梯形的周长为AD+DC+BC+AB=5+5+11+5=26.
(2)证明:如上图,设A,D在BC上的垂线的垂足分别是E,F.AC,BD交于O.
则BE=FC=2.DF=
=
=5.
从而△BFD为等腰直角三角形.∠DBF=45°
同理:∠ACE=45°,得∠BOC=90°.
∴AC⊥BD.
 解:(1)如图,过点A作AE⊥BC,
解:(1)如图,过点A作AE⊥BC,∴AE=4,又AD=5,BC=11,∴BE=
| 1 |
| 2 |
∴CD=AB=5,
∴梯形的周长为AD+DC+BC+AB=5+5+11+5=26.
(2)证明:如上图,设A,D在BC上的垂线的垂足分别是E,F.AC,BD交于O.
则BE=FC=2.DF=
| (BD2-BF2) |
| 50-25 |
从而△BFD为等腰直角三角形.∠DBF=45°
同理:∠ACE=45°,得∠BOC=90°.
∴AC⊥BD.
点评:熟练掌握等腰梯形的性质,会在梯形中运用其性质进行一些简单的计算.

练习册系列答案
相关题目
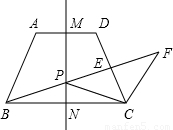
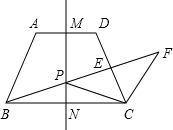 的对称轴,点P是线段MN上一个动点(不与M、N重合),射线BP交线段CD于点E,过点C作CF∥AB交射线BP于点F.
的对称轴,点P是线段MN上一个动点(不与M、N重合),射线BP交线段CD于点E,过点C作CF∥AB交射线BP于点F.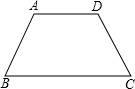 已知如图,在等腰梯形ABCD中,AD∥BC.
已知如图,在等腰梯形ABCD中,AD∥BC. ,证明:AC⊥BD.
,证明:AC⊥BD.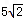 ,证明:AC⊥BD。
,证明:AC⊥BD。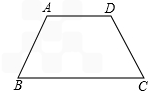
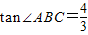 ,直线MN是梯形的对称轴,点P是线段MN上一个动点(不与M、N重合),射线BP交线段CD于点E,过点C作CF∥AB交射线BP于点F.
,直线MN是梯形的对称轴,点P是线段MN上一个动点(不与M、N重合),射线BP交线段CD于点E,过点C作CF∥AB交射线BP于点F.