题目内容
已知如图,在等腰梯形ABCD中,AD∥BC。
(1)若AD=5,BC=11,梯形的高是4,求梯形的周长;
(2)若AD=3,BC=7,BD=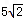 ,证明:AC⊥BD。
,证明:AC⊥BD。
(1)若AD=5,BC=11,梯形的高是4,求梯形的周长;
(2)若AD=3,BC=7,BD=
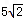 ,证明:AC⊥BD。
,证明:AC⊥BD。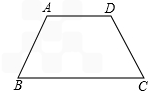
|
解:(1)如图,过点A作AE?BC, |
 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
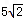 ,证明:AC⊥BD。
,证明:AC⊥BD。
|
解:(1)如图,过点A作AE?BC, |
 |

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案