题目内容
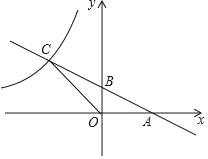
【题目】如图,直线y=-![]() x+b(b>0)与x轴、y轴分别交于点A、B,与双曲线y=-
x+b(b>0)与x轴、y轴分别交于点A、B,与双曲线y=-![]() (x<0)交于点C.
(x<0)交于点C.
(1)若△AOB的面积为2,求b的值;
(2)连接OC,若△AOC的面积为2,求b的值.
【答案】(1)![]() ;(2)1.
;(2)1.
【解析】
(1)由点A、B在直线y=﹣![]() x+b上,可求出A、B两点的坐标,再根据三角形面积即可求出b的值.(2)过C作CH⊥AO于H,则S△CHO=
x+b上,可求出A、B两点的坐标,再根据三角形面积即可求出b的值.(2)过C作CH⊥AO于H,则S△CHO=![]() |4|=2,由△AOC的面积为2可知OH=AO=2b,根据点C在直线上即可求出b值.
|4|=2,由△AOC的面积为2可知OH=AO=2b,根据点C在直线上即可求出b值.
(1)∵y=﹣![]() x+b,令x=0,则y=b;令y=0,则x=2b,
x+b,令x=0,则y=b;令y=0,则x=2b,
∴A(2b,0),B(0,b),
∴S△AOB=![]() OAOB=
OAOB=![]() b×2b=2,
b×2b=2,
∴b2=2,
又∵b>0,
∴b=![]() ;
;
(2)如图,过C作CH⊥AO于H,
∵S△CHO=![]() |4|=2,△AOC的面积为2,
|4|=2,△AOC的面积为2,
∴OH=AO=2b,
设C(﹣2b,![]() ),且点C在直线上,
),且点C在直线上,
∴﹣![]() ×(﹣2b)+b=
×(﹣2b)+b=![]() ,
,
∴b2=1,
又∵b>0,
∴b=1.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目