Question

【题目】如图，矩形ABCD中，AB=6，BC=6，动点P从点A出发，以每秒 个单位长度的速度沿线段AD运动，动点Q从点D出发，以每秒2个单位长度的速度沿折线段D﹣O﹣C运动，已知P、Q同时开始移动，当动点P到达D点时，P、Q同时停止运动．设运动时间为t秒．

（1）当t=1秒时，求动点P、Q之间的距离；

（2）若动点P、Q之间的距离为4个单位长度，求t的值；

（3）若线段PQ的中点为M，在整个运动过程中；直接写出点M运动路径的长度为　　．

Answer 1

【答案】（1）7；（2），t=2或4s时，PQ=4；（3）.

【解析】

（1）作QK⊥AD于K．根据矩形性质可知tan∠BDA=，所以∠BDA=30°，当t=1时，DQ=2，QK=DQ=1，DK=，根据勾股定理求出PQ长即可.（2）分两种情况讨论：①当0＜t≤3时，QK=t，PK=6﹣2t，已知PQ=4，所以t2+（6﹣2t）2=42，求出t的值即可. ②当3＜t≤6时，作QH⊥AD于H，OK⊥AD于K，OF⊥OH于F．根据根据矩形性质可知OD+OQ=AQ=2t，AH=t， 已知AP=t，所以点P与点H重合，由PQ=4即可求出t的值.（3）作OK⊥AD于K．QH⊥AD于H．由矩形性质可知OD=OA，由OK⊥AD得DK=AK，根据DH=PA=t得KH=PK因为MK∥HQ，MQ=MP，所以点M在OD上时的运动距离为OK=．当点Q在线段OC上时，取CD的中点M′，OK的中点M，连接MM′，则点M的运动轨迹是线段MM′．根据勾股定理求出MM′的长即可，在整个运动过程中点M运动路径的长度为MM′+.

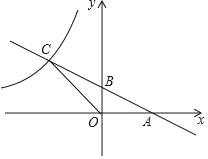
（1）如图1中，作QK⊥AD于K．

∵四边形ABCD是矩形，

∴BC=AD=6，∠BAD=90°，

∴tan∠BDA=，

∴∠BDA=30°，

当t=1时，DQ=2，QK=DQ=1，DK=，

∵PA=，

∴PK=4，

∴PQ= =7．

（2）①如图1中，当0＜t≤3时，QK=t，PK=6﹣2t，

∵PQ=4，

∴t2+（6﹣2t）2=42，

解得t=2或（舍弃）

②如图2中，当3＜t≤6时，作QH⊥AD于H，OK⊥AD于K，OF⊥OH于F．

由题意：AQ=2t，AH=t，

∵AP=t，

∴AH=AP，

∴P与H重合，

当PQ=4时，AQ=8，

∴2t=8，

∴t=2，

综上所述，t=2或4s时，PQ=4．

（3）如图3中，作OK⊥AD于K．QH⊥AD于H．

∵四边形ABCD是矩形，

∴OD=OA，

∵OK⊥AD，

∴DK=AK，

∵DH=PA=t，

∴KH=PK，

∵MK∥HQ，MQ=MP，

∴点M在线段OK上，当点Q从D到O时，点M的运动距离=OK=，

如图4中，当点Q在线段OC上时，取CD的中点M′，OK的中点M，连接MM′，则点M的运动轨迹是线段MM′．

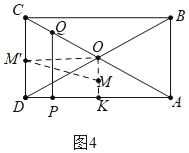
在Rt△OMM′中，MM′= =，

∴在整个运动过程中；直接写出点M运动路径的长度为.

故答案为．