题目内容
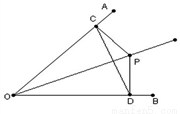
8. 如图所示,在锐角△ABC中,高CD、BE相交于点F.
如图所示,在锐角△ABC中,高CD、BE相交于点F.(1)指出图中所有的相似三角形,并证明一对三角形相似;
(2)连结DE,试说明:△ADE∽△ACB.
分析 (1)根据垂直的定义得到∠AEB=∠ADC=90°,根据有两组角对应相等的两个三角形相似证明结论;
(2)根据∠AEB=∠ADC=90°,得到E、D、B、C四点共圆,根据圆内接四边形的性质得到∠ADE=∠ACB,证明结论.
解答 解:(1)△AEB∽△ADC,△CFE∽△BFD;
∵BE⊥AC,CD⊥AB,
∴∠AEB=∠ADC=90°,
又∵∠A=∠A,
∴△AEB∽△ADC;
(2)∵∠AEB=∠ADC=90°,
∴E、D、B、C四点共圆,
∴∠ADE=∠ACB,
又∵∠A=∠A,
∴△ADE∽△ACB.
点评 本题考查的是相似三角形的判定,掌握有两组角对应相等的两个三角形相似是解题的关键.

练习册系列答案
相关题目
 的非负整数解是__________________
的非负整数解是__________________
 某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2).那么最后一名同学的位置对应的坐标是(4,-1),全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是(12,-22).
某班共有52名同学,在校广播操比赛中排成方队,先把每位同学都进行编号,然后把各自的位置固定下来,如图,在平面直角坐标系中,每个自然数都对应着一个坐标.例如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2).那么最后一名同学的位置对应的坐标是(4,-1),全校学生如果排成这样一个大方阵,编号是2015的学生的对应点的坐标是(12,-22).