题目内容
1.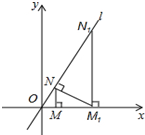 如图,已知直线l:y=$\sqrt{3}x$(直线l与x轴的夹角是60°),过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点Mn的坐标为(22n+1,0).
如图,已知直线l:y=$\sqrt{3}x$(直线l与x轴的夹角是60°),过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点Mn的坐标为(22n+1,0).
分析 根据直线l的解析式求出∠MON=60°,从而得到∠MNO=∠OM1N=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出OM1=22•OM,然后表示出OMn与OM的关系,再根据点Mn在x轴上写出坐标即可.
解答 解:∵直线l:y=$\sqrt{3}$x,
∴∠MON=60°,
∵NM⊥x轴,M1N⊥直线l,
∴∠MNO=∠OM1N=90°-60°=30°,
∴ON=2OM,OM1=2ON=4OM=22•OM,
同理,OM2=22•OM1=(22)2•OM,
…,
OMn=(22)n•OM=22n•2=22n+1,
所以,点Mn的坐标为(22n+1,0).
故答案为:(22n+1,0).
点评 本题考查了一次函数图象上点的坐标特征,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质并求出变化规律是解题的关键.

练习册系列答案
相关题目
6.某车间56名工人,每人每天能生产螺栓16个或螺母24个,设有x名工人生产螺栓,有y名工人生产螺母,每天生产的螺栓和螺母按1:2配套,所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=56}\\{2×16x=24y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=56}\\{2×24x=26y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=56}\\{16x=24y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=56}\\{24x=16y}\end{array}\right.$ |
13.某景点的门票价格如下表:
某校八年级(一)、(二)两班共102人去游览该景点,其中(一)班不足50人,(二)班多于50人但不足60人,如果两班都以班为单位分别购票,则一共付款1118元.
(1)两班各有多少名学生?
(2)如果你是购票决策人,将如何购票能够省钱?可节省多少钱?
| 购票人数 | 1~50人 | 51~100人 | 100人以上 |
| 每人门票价 | 12元 | 10元 | 8元 |
(1)两班各有多少名学生?
(2)如果你是购票决策人,将如何购票能够省钱?可节省多少钱?
10.将点A(-3,-2)向左平移5个单位,再向下平移4个单位得到点B,则点B的坐标为( )
| A. | (-8,2) | B. | (-8,-6) | C. | (2,-2) | D. | (2,2) |
11.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | $\sqrt{12}$÷$\sqrt{3}$=4 |
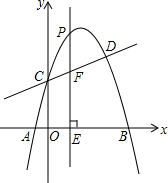 如图,抛物线y=ax2+$\frac{7}{2}$x+c与直线y=kx+2交于C,D两点,其中点C在y轴上,点D的坐标为(3,$\frac{7}{2}$).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
如图,抛物线y=ax2+$\frac{7}{2}$x+c与直线y=kx+2交于C,D两点,其中点C在y轴上,点D的坐标为(3,$\frac{7}{2}$).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.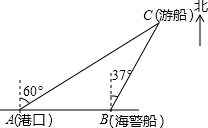 一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向.
一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向. (1)已知关于x的一元二次方程x2-4x+m-1=0有两个相等的实数根,求m的值及方程的根.
(1)已知关于x的一元二次方程x2-4x+m-1=0有两个相等的实数根,求m的值及方程的根.