题目内容
 如图所示,已知:在△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,AB=12cm,则BD=
如图所示,已知:在△ABC中,∠ACB=90°,CD⊥AB,∠A=30°,AB=12cm,则BD=考点:含30度角的直角三角形
专题:
分析:根据在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,即可求出BC长,再根据∠BCD=∠A=30°即可求出BD的长.
解答:解:∵△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,
∴BC=
AB=6cm,
又∵∠BCD=∠A=30°,
∴在直角△BCD中,BD=
BC=3cm.
故答案为:3.
∴BC=
| 1 |
| 2 |
又∵∠BCD=∠A=30°,
∴在直角△BCD中,BD=
| 1 |
| 2 |
故答案为:3.
点评:此题考查的知识点是含30度角的直角三角形,关键是熟记含30°的直角三角形的性质,即30°锐角所对的直角边是斜边的一半.

练习册系列答案
相关题目
已知
=
,那么
、
、
的大小关系是( )
| a+b |
| b |
| 7 |
| 3 |
| a |
| b |
| a-b |
| b |
| a+b |
| a-b |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
身高相同的甲、乙、丙三人放风筝,各人放出线长分别为300米、350米、280米,线与地面的夹角分别为30°、45°、60°(假设风筝线是拉直的),三人所放风筝( )
| A、甲的最高 | B、乙的最高 |
| C、丙的最高 | D、一样高 |
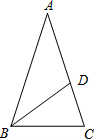 如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点.
如图,已知等腰△ABC中,顶角∠A=36°,BD为∠ABC的平分线,求证:点D是AC的黄金分割点. 如图,已知⊙O的半径为2cm,弦AB=2cm,P点为弦AB上一动点,则线段OP的范围是
如图,已知⊙O的半径为2cm,弦AB=2cm,P点为弦AB上一动点,则线段OP的范围是