题目内容
教你一招：把a2-2ab+b2-c2因式分解．
解：原式=（a2-2ab+b2）-c2
=（a-b）2-c2
=（a-b+c）（a-b-c）
请你仔细阅读上述解法后，把下列多项式因式分解：-a2+4x2-4xy+y2．
解：原式=（a2-2ab+b2）-c2
=（a-b）2-c2
=（a-b+c）（a-b-c）
请你仔细阅读上述解法后，把下列多项式因式分解：-a2+4x2-4xy+y2．
考点：因式分解-分组分解法
专题：阅读型
分析：将后三项分组，进而利用完全平方公式以及平方差公式分解因式得出即可．
解答：解：-a2+4x2-4xy+y2
=4x2-4xy+y2-a2
=（2x-y）2-a2
=（2x-y+a）（2x-y-a）．
=4x2-4xy+y2-a2
=（2x-y）2-a2
=（2x-y+a）（2x-y-a）．
点评：此题主要考查了分组分解法以及公式法分解因式，正确分组得出是解题关键．
练习册系列答案
相关题目
一个圆锥的母线长为8，侧面展开图是半圆，则这个圆锥的高是（ ）
| A、4 | ||
B、4
| ||
C、4
| ||
D、2
|
如图，加条件能满足AAS来判断△ACD≌△ABE的条件是（ ）| A、∠AEB=∠ADC，∠C=∠D |
| B、∠AEB=∠ADC，CD=BE |
| C、AC=AB，AD=AE |
| D、AC=AB，∠C=∠B |
已知．在Rt△OAB中，∠OAB=90°，∠BOA=30°，OA=2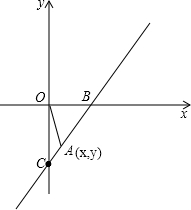
如图，y=2x-1与x轴、y轴分别交于B、C两点，点A（x，y）是第四象限内的直线y=2x-1上的一个动点．