Question

【题目】如图，是反比例函数在第一象限图像上一点，连接，过作轴，截取（在右侧），连接，交反比例函数的图像于点．

（1）求反比例函数的表达式；

（2）求点的坐标及所在直线解析式；

（3）求的面积．

Answer 1

【答案】（1）y=；（2）B（18，6），y=x；（3）20．

【解析】

（1）直接代入A点坐标即可求出k的值，进而可得函数解析式；
（2）过点A作AD⊥x轴于点D，利用勾股定理计算出AO的长，进而可得AB长，然后可得B点坐标．设OB所在直线解析式为y=mx（m≠0）利用待定系数法可求出BO的解析式；
（3）首先联立两个函数解析式，求出C点坐标，过点C作CE⊥x轴，延长EC交AB于点F，连接AC，再确定F点坐标，最后求面积即可．

解：（1）将点A（8，6）代入（k≠0），
得：k=48，
则反比例函数解析式为y=；
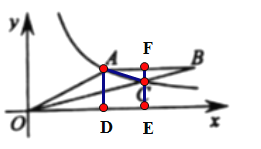
（2）如图，过点A作AD⊥x轴于点D，
则OD=8、AD=6，
∴OA==10，
∵AB∥x轴，且AB=OA=10，
∴点B的坐标为（18，6）；
设OB所在直线解析式为y=mx（m≠0），
将点B（18，6）代入得m= ，
∴OB所在直线解析式为y=x；
（3）联立解析式：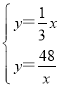

解得： ，
可得点C坐标为（12，4），
过点C作CE⊥x轴，延长EC交AB于点F，连接AC，
则点F坐标为（12，6），
∴AF=4，CF=2，CE=4，
则△OAC的面积=×（4+12）×6-×12×4-×4×2=20．