Question

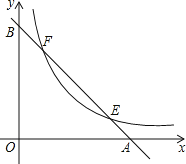
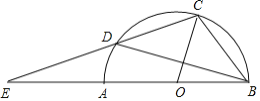
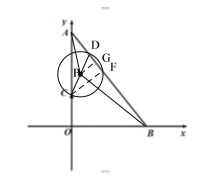
【题目】如图，在平面直角坐标系中，点从点运动到点停止，连接，以长为直径作.

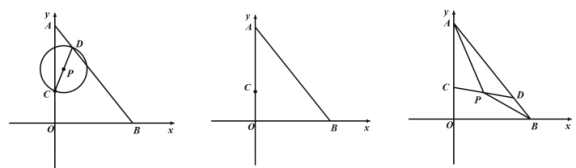
（1）若，求的半径；

（2）当与相切时，求的面积；

（3）连接，在整个运动过程中，的面积是否为定值，如果是，请直接写出面积的定值，如果不是，请说明理由.

Answer 1

【答案】（1）；（2）；（3）是，

【解析】

（1）若，则 ,代入数值即可求得CD,从而求得的半径.

（2）当与相切时，则CD⊥AB，利用△ACD∽△ABO，得出比例式求得CD，AD的长，过P点作PE⊥AO于E点，再利用△CPE∽△CAD，得出比例式求得P点的坐标，即可求得△POB的面积.

（3）①若 与AB有一个交点，则与AB相切，由（2）可得PD⊥AB，PD= ,则 ②若 与AB有两个交点，设另一个交点为F，连接CF,则∠CFD=90°，由（2）可得CF=3，过P点作PG⊥AB于G点，则DG= ，PG为△DCF的中位线，PG= , 则,综上所述，△PAB的面积是定值，为 .

（1）根据题意得：OA=8，OB=6，OC=3

∴AC=5

∵

∴

即

∴CD=

∴ 的半径为

（2）在直角三角形AOB中，OA=8，OB=6，

∴AB= ，

当与相切时，CD⊥AB，

∴∠ADC=∠AOB=90°，∠CAD=∠BAO

∴△ACD∽△ABO

∴ ，即

∴CD=3，AD=4

∵CD为圆P的直径

∴CP=

过P点作PE⊥AO于E点，

则∠PEC=∠ADC=90°，∠PCE=∠ACD

∴△CPE∽△CAD

∴

即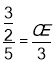

∴CE=

∴OE=

故P点的纵坐标为

∴△POB的面积=

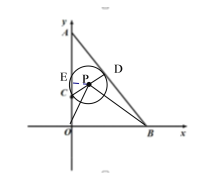
（3）①若 与AB有一个交点，则与AB相切，

由（2）可得PD⊥AB，PD= ,则

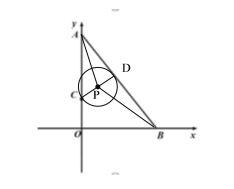
②若 与AB有两个交点，设另一个交点为F，连接CF,则∠CFD=90°，

由（2）可得CF=3，

过P点作PG⊥AB于G点，则DG= ，PG为△DCF的中位线，PG= ,

则.

综上所述，△PAB的面积是定值，为 .