题目内容
5．方程x+2y=7在正整数范围内的解有（ ）| A． | 1个 | B． | 3个 | C． | 4个 | D． | 无数个 |
分析 由于二元一次方程x+2y=7中x的系数是1，可先用含y的代数式表示x，然后根据此方程的解是正整数，那么把最小的正整数y=1代入，算出对应的x的值，再把y=2代入，再算出对应的x的值，依此可以求出结果．
解答 解：∵x+2y=7，
∴x=7-2y，
∵x、y都是正整数，
∴y=1时，x=5；
y=2时，x=3；
y=3时，x=1．
∴方程x+2y=7在正整数范围内的解有3对．
故选B．
点评 考查了二元一次方程的解，由于任何一个二元一次方程都有无穷多个解，求满足二元一次方程的正整数解，即此方程中两个未知数的值都是正整数，这是解答本题的关键．注意最小的正整数是1．
练习册系列答案
相关题目
13．若a＞b，则下列不等式不一定成立的是（ ）
| A． | a+m＞b+m | B． | a（m2+1）＞b（m2+1） | C． | -2a＜-2b | D． | a2＞b2 |
10．下列方程组中，是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{xy=1}\\{x+2y=3}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=2}\\{3y-x=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{\frac{1}{x}+\frac{1}{y}=1}\\{x+y=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+z=2}\\{x+y=3}\end{array}\right.$ |
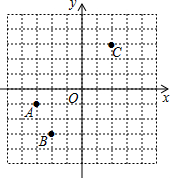点A，B，C在如图所示的平面直角坐标系内，按要求完成下列各小题．