题目内容
11.使等式$\sqrt{\frac{x+1}{x-3}}=\frac{\sqrt{x+1}}{\sqrt{x-3}}$成立的条件是( )| A. | x>-1且x≠3 | B. | x≥-1且x≠3 | C. | x>3 | D. | x≥3 |
分析 利用二次根式的性质得出x+1≥0,x-3>0,进而得出答案.
解答 解:∵$\sqrt{\frac{x+1}{x-3}}=\frac{\sqrt{x+1}}{\sqrt{x-3}}$,
∴x+1≥0,x-3>0,
解得:x>3.
故选:C.
点评 此题主要考查了二次根式的性质,根据题意得出关于x的不等式是解题关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
19.下列说法正确的有( )个
(1)同位角相等
(2)两条边和其中一条边的对角对应相等的两个三角形全等
(3)“两个负数的和是正数”是确定事件
(4)角的对称轴是他的角平分线
(5)三角形的最大内角不小于60度.
(1)同位角相等
(2)两条边和其中一条边的对角对应相等的两个三角形全等
(3)“两个负数的和是正数”是确定事件
(4)角的对称轴是他的角平分线
(5)三角形的最大内角不小于60度.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.下列多项式能用公式进行分解因式的是( )
| A. | x2+y2 | B. | -x2-y2 | C. | x2+4xy+4y2 | D. | x2+xy+y2 |
3.将方程2x2=3-5x化为一般形式,a,b,c的值分别为( )
| A. | a=2,b=5,c=3 | B. | a=2,b=-5,c=3 | C. | a=2,b=5,c=-3 | D. | a=2,b=-5,c=-3 |
 用三角尺画角平分线:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,再分别用三角尺过M、N作OA,OB的垂线,交点为P,画射线OP,则这条射线即为∠AOB的平分线.请解释这种画角平分线方法的道理.
用三角尺画角平分线:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,再分别用三角尺过M、N作OA,OB的垂线,交点为P,画射线OP,则这条射线即为∠AOB的平分线.请解释这种画角平分线方法的道理.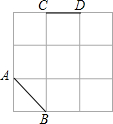 操作题:如图,在3×3网格中,已知线段AB、CD,以格点为端点画一条线段,使它与AB、CD组成轴对称图形.(画出所有可能)
操作题:如图,在3×3网格中,已知线段AB、CD,以格点为端点画一条线段,使它与AB、CD组成轴对称图形.(画出所有可能)