ћвƒњƒЏ»Ё
°Њћвƒњ°њ“їћмЌн…ѕ£ђ–°јцЇЌ–°ї™‘Џєг≥°…ѕ…Ґ≤љ£ђњіЉыєг≥°…ѕ”–“ї¬Јµ∆ЄЋ![]() £®»зЌЉ£©£ђ∞Ѓґѓƒ‘љоµƒ–°јцЇЌ–°ї™ѕлјы”√Ќґ”∞÷™ ґјі≤вЅњ¬Јµ∆ЄЋ
£®»зЌЉ£©£ђ∞Ѓґѓƒ‘љоµƒ–°јцЇЌ–°ї™ѕлјы”√Ќґ”∞÷™ ґјі≤вЅњ¬Јµ∆ЄЋ![]() µƒЄяґ»£Ѓ«лњіѕ¬√жµƒ“їґќґ‘ї∞£Ѓ
µƒЄяґ»£Ѓ«лњіѕ¬√жµƒ“їґќґ‘ї∞£Ѓ
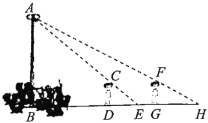
–°јц£Ї–°ї™£ђƒг’Њ‘Џµг![]() і¶£ђќ“Ѕњµ√ƒгµƒ”∞≥§
і¶£ђќ“Ѕњµ√ƒгµƒ”∞≥§![]() «4m£ї»їЇуƒг‘ў—Ў„≈÷±ѕя
«4m£ї»їЇуƒг‘ў—Ў„≈÷±ѕя![]() „яµљµг
„яµљµг![]() і¶£ђ”÷Ѕњµ√
і¶£ђ”÷Ѕњµ√![]() ќ™6m£ђіЋ ±ƒгµƒ”∞≥§
ќ™6m£ђіЋ ±ƒгµƒ”∞≥§![]() “≤ «6m£Ѓ
“≤ «6m£Ѓ
–°ї™£Ї„тћмћеЉм ±£ђ“љ…ъЋµќ“µƒ…нЄя «1.6m£Ѓ
«лƒгЄщЊЁЋэ√«µƒґ‘ї∞Љ∞ Њ“вЌЉ£ђ«у≥ц¬Јµ∆ЄЋ![]() µƒЄяґ»
µƒЄяґ»
°Њір∞Є°њ¬Јµ∆ЄЋ![]() µƒЄяґ»ќ™6.4m£Ѓ
µƒЄяґ»ќ™6.4m£Ѓ
°Њљвќц°њ
ЄщЊЁAB°ЌBH£ђCD°ЌBH£ђFG°ЌBH£ђњ…µ√£Ї°чABE°„°чCDE£ђ‘т”–![]() ЇЌ
ЇЌ![]() £ђґш
£ђґш![]() £ђЉі
£ђЉі![]() £ђі”ґш«у≥цBDµƒ≥§£ђ‘ўіъ»л«∞√ж»ќ“в“їЄцµ» љ÷–£ђЉіњ…«у≥цAB£Ѓ
£ђі”ґш«у≥цBDµƒ≥§£ђ‘ўіъ»л«∞√ж»ќ“в“їЄцµ» љ÷–£ђЉіњ…«у≥цAB£Ѓ
ЄщЊЁћв“в£ђµ√![]() £ђ
£ђ![]() £ђ
£ђ![]() £Ѓ
£Ѓ
‘Џ![]() ЇЌ
ЇЌ![]() ÷–£ђ
÷–£ђ
°я![]() £ђ
£ђ![]() £ђ°а
£ђ°а![]() £ђ
£ђ
°а![]() £ђ°а
£ђ°а![]() £ЃҐў
£ЃҐў
Ќђјн£ђ‘Џ![]() ЇЌ
ЇЌ![]() ÷–£ђ
÷–£ђ![]() £ЃҐЏ
£ЃҐЏ
”÷°я![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ
°я![]()
°а![]() £ђ
£ђ
Љі![]() £Ѓ
£Ѓ
љвµ√![]() £ђљЂ
£ђљЂ![]() іъ»лҐў£ђ
іъ»лҐў£ђ
Љі![]() £ђљвµ√
£ђљвµ√![]() £Ѓ
£Ѓ
Њ≠Љм—й£ђ![]() £ђ
£ђ![]() «‘≠Ј÷ љЈљ≥ћµƒљв£Ѓ
«‘≠Ј÷ љЈљ≥ћµƒљв£Ѓ
ір£Ї¬Јµ∆ЄЋ![]() µƒЄяґ»ќ™6.4m£Ѓ
µƒЄяґ»ќ™6.4m£Ѓ

 ћмћмѕт…ѕ“ї±ЊЇ√ЊнѕµЅ–ір∞Є
ћмћмѕт…ѕ“ї±ЊЇ√ЊнѕµЅ–ір∞Є –°—І…ъ10Ј÷÷””¶”√ћвѕµЅ–ір∞Є
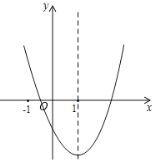
–°—І…ъ10Ј÷÷””¶”√ћвѕµЅ–ір∞Є°Њћвƒњ°њ‘Џї≠ґюіќЇѓ э![]() µƒЌЉѕу ±£ђЉ„–іінЅЋ“їіќѕоµƒѕµ э£ђЅ–±н»зѕ¬
µƒЌЉѕу ±£ђЉ„–іінЅЋ“їіќѕоµƒѕµ э£ђЅ–±н»зѕ¬
| °≠°≠ | ©Б1 | 0 | 1 | 2 | 3 | °≠°≠ |
| °≠°≠ | 6 | 3 | 2 | 3 | 6 | °≠°≠ |
““–іінЅЋ≥£ эѕо£ђЅ–±н»зѕ¬£Ї
| °≠°≠ | ©Б1 | 0 | 1 | 2 | 3 | °≠°≠ |
| °≠°≠ | ©Б2 | ©Б1 | 2 | 7 | 14 | °≠°≠ |
Ќ®єэ…ѕ ц–≈ѕҐ£ђљвЊц“‘ѕ¬ќ ћв£Ї
(1)«у‘≠ґюіќЇѓ э![]() µƒ±ніп љ£ї
µƒ±ніп љ£ї
(2)ґ‘”ЏґюіќЇѓ э![]() £ђµ±
£ђµ±![]() _____ ±£ђ
_____ ±£ђ![]() µƒ÷µЋж
µƒ÷µЋж![]() µƒ÷µ‘ціуґш‘ціу£ї
µƒ÷µ‘ціуґш‘ціу£ї
(3)»фєЎ”Џ![]() µƒЈљ≥ћ
µƒЈљ≥ћ![]() ”–ЅљЄц≤їѕаµ»µƒ µ эЄщ£ђ«у
”–ЅљЄц≤їѕаµ»µƒ µ эЄщ£ђ«у![]() µƒ»°÷µЈґќІ£Ѓ
µƒ»°÷µЈґќІ£Ѓ