题目内容
18.下列各组数中,不能组成直角三角形的是( )| A. | 7,24,25 | B. | 9,12,15 | C. | 1,$\sqrt{2}$,3 | D. | 5,12,13 |
分析 根据勾股定理的逆定理对四个选项中所给的数据看是否符合两个较小数的平方和等于最大数的平方即可.
解答 解:A、72+242=252,能构成直角三角形,不符合题意;
B、92+122=152,能构成直角三角形,不符合题意;
C、12+($\sqrt{2}$)2≠32,不能构成直角三角形,符合题意;
D、52+122=132,能构成直角三角形,不符合题意.
故选C.
点评 本题考查的是勾股定理的逆定理,即如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
13.能使分式方程$\frac{k}{1-x}$+2=$\frac{3}{x-1}$有非负实数解且使一次函数y=(k+2)x-1的图象不经过第一象限的所有整数k的积为( )
| A. | 20 | B. | -20 | C. | 60 | D. | -60 |
10.九年级数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价y(单位:元/件)与时间x(单位:天)的函数关系式为y=$\left\{\begin{array}{l}{x+40(0≤x≤50,且x为整数)}\\{90(50<x≤90,且x为整数)}\end{array}\right.$;在第x天的销售量p(单位:件)与时间x(单位:天)的函数关系的相关信息如表.已知商品的进价为30元/件,每天的销售利润为w(单位:元).
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?
| 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量p(件) | 198 | 140 | 80 | 20 |
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?
8.用四舍五入法对2.098176分别取近似值,其中正确的是( )
| A. | 2.09(精确到0.01) | B. | 2.098(精确到千分位) | ||
| C. | 2.0(精确到十分位) | D. | 2.0981(精确到0.0001) |
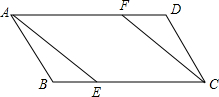 如图,在?ABCD中,点E、F分别在边BC和AD上,且BE=DF.求证:AE=CF.
如图,在?ABCD中,点E、F分别在边BC和AD上,且BE=DF.求证:AE=CF.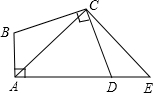 如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=CD,E是AD延长线上一点,若DE=AB=3cm,CE=4$\sqrt{2}$cm,连接AC,BD.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=CD,E是AD延长线上一点,若DE=AB=3cm,CE=4$\sqrt{2}$cm,连接AC,BD.