题目内容
3.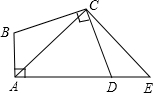 如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=CD,E是AD延长线上一点,若DE=AB=3cm,CE=4$\sqrt{2}$cm,连接AC,BD.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=CD,E是AD延长线上一点,若DE=AB=3cm,CE=4$\sqrt{2}$cm,连接AC,BD.(1)求证:△BCD∽△ACE;
(2)试求出线段AD的长.
分析 (1)根据四边形的内角和等于360°求出∠B+∠ADC=180°,再根据邻补角的和等于180°可得∠CDE+∠ADE=180°,从而求出∠B=∠CDE,然后根据“边角边”得出AC=CE进而得出结论;
(2)根据全等三角形对应边相等可得AC=EC,全等三角形对应角相等可得∠ACB=∠ECD,然后求出∠ACE=90°,得到△ACE是等腰直角三角形,求出AE的长度,再根据AD=AE-DE代入数据进行计算即可得解.
解答 解:(1)证明:在四边形ABCD中,∵∠BAD=∠BCD=90°,
∴90°+∠B+90°+∠ADC=360°,
∴∠B+∠ADC=180°,
又∵∠CDE+∠ADE=180°,
∴∠B=∠CDE,
在△ABC和△EDC中,$\left\{\begin{array}{l}{AB=DE}\\{∠B=∠CDE}\\{BC=CD}\end{array}\right.$,
∴△ABC≌△EDC(SAS);
∴AC=CE,
∵BC=CD
∴$\frac{BC}{AC}=\frac{CD}{EC}$,
∵∠BAD=∠BCD=90°,
∴△BCD∽△ACE.
(2)解:∵△ABC≌△EDC,
∴AC=EC,∠ACB=∠ECD,
∵∠BCD=∠ACB+∠ACD=90°,
∴∠ACE=∠ECD+∠ACD=90°,
∴△ACE是等腰直角三角形,
∵CE=4$\sqrt{2}$cm,
∴AE=4$\sqrt{2}$×$\sqrt{2}$=8cm,
∴AD=AE-DE=8-3=5cm.
点评 此题是相似三角形的性质和判定,主要考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,根据四边形的内角和定理以及邻补角的定义,利用同角的补角相等求出夹角相等是证明三角形全等的关键,也是本题的难点.

练习册系列答案
相关题目
18.下列各组数中,不能组成直角三角形的是( )
| A. | 7,24,25 | B. | 9,12,15 | C. | 1,$\sqrt{2}$,3 | D. | 5,12,13 |
12.某食堂购进30袋大米,每袋以50千克为标准,超过的记为正,不足的记为负,称重记录如表.
(1)这30袋大米的总重量比标准总重量是多还是少?相差多少?
(2)大米单价是每千克5.5元,食堂购进大米总共花多少钱?
| 与标准重量偏差(单位:千克) | -2 | -1 | 0 | 1 | 2 | 3 |
| 袋 数 | 5 | 10 | 3 | 1 | 5 | 6 |
(2)大米单价是每千克5.5元,食堂购进大米总共花多少钱?
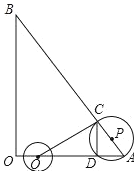 如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.