题目内容
5.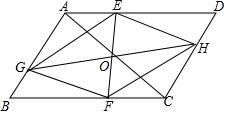 如图,在?ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E、F,GH过点O,与AB,CD分别相交于点G、H,连接EG、FG、FH、EH.求证:四边形EGFH是平行四边形.
如图,在?ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E、F,GH过点O,与AB,CD分别相交于点G、H,连接EG、FG、FH、EH.求证:四边形EGFH是平行四边形.
分析 由四边形ABCD是平行四边形,得到AD∥BC,根据平行四边形的性质得到∠EAO=∠FCO,证出△OAE≌△OCF,得到OE=OF,同理OG=OH,根据对角线互相平分的四边形是平行四边形得到结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAO=∠FCO,
在△OAE与△OCF中,$\left\{\begin{array}{l}{∠EAO=∠FCO}&{\;}\\{∠AOE=∠COF}&{\;}\\{OA=OC}&{\;}\end{array}\right.$,
∴△OAE≌△OCF(AAS),
∴OE=OF,
同理OG=OH,
∴四边形EGFH是平行四边形;
点评 本题考查了平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握平行四边形的判定定理是解题的关键.

练习册系列答案
相关题目
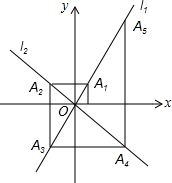 如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009),A2n+1的坐标为((-2)n,2(-2)n).
如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009),A2n+1的坐标为((-2)n,2(-2)n). 如图,以AB为直径的⊙O交△ABC的BC、AC边与D、E两点,在图中仅以没有刻度的直尺画出三角形的三条高(简单叙述你的画法).
如图,以AB为直径的⊙O交△ABC的BC、AC边与D、E两点,在图中仅以没有刻度的直尺画出三角形的三条高(简单叙述你的画法).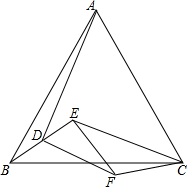 如图,在△ABC中,AB=AC,在△EFC中,EF=FC,且∠BAC+∠EFC=180°,D是BE中点.求证:AD⊥DF.
如图,在△ABC中,AB=AC,在△EFC中,EF=FC,且∠BAC+∠EFC=180°,D是BE中点.求证:AD⊥DF.