题目内容
10.平面直角坐标系xOy中有四点A(-2,0),B(-1,0),C(0,1),D(0,2)在A、B、C、D中取两点与点O为顶点作三角形,所作三角形是等腰直角三角形的概率是$\frac{1}{2}$.分析 根据题意得到在A、B、C、D中取两点与点O为顶点作三角形一共可作4个三角形,其中所作三角形是等腰直角三角形的有2个,如何根据概率公式即可得到结论.
解答  解:如图,在A、B、C、D中取两点与点O为顶点作三角形一共可作4个三角形,
解:如图,在A、B、C、D中取两点与点O为顶点作三角形一共可作4个三角形,
其中所作三角形是等腰直角三角形的有2个,
∴P(所作三角形是等腰直角三角形)=$\frac{2}{4}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.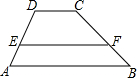 如图,在四边形ABCD中,E,F分别在AD和BC上,AB∥EF∥DC,且DE=3,DA=5,CF=4,则FB等于( )
如图,在四边形ABCD中,E,F分别在AD和BC上,AB∥EF∥DC,且DE=3,DA=5,CF=4,则FB等于( )
 如图,在四边形ABCD中,E,F分别在AD和BC上,AB∥EF∥DC,且DE=3,DA=5,CF=4,则FB等于( )
如图,在四边形ABCD中,E,F分别在AD和BC上,AB∥EF∥DC,且DE=3,DA=5,CF=4,则FB等于( )| A. | $\frac{3}{2}$ | B. | $\frac{8}{3}$ | C. | 5 | D. | 6 |
5.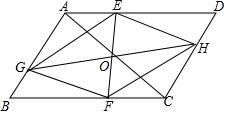 如图,在?ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E、F,GH过点O,与AB,CD分别相交于点G、H,连接EG、FG、FH、EH.求证:四边形EGFH是平行四边形.
如图,在?ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E、F,GH过点O,与AB,CD分别相交于点G、H,连接EG、FG、FH、EH.求证:四边形EGFH是平行四边形.
 如图,在?ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E、F,GH过点O,与AB,CD分别相交于点G、H,连接EG、FG、FH、EH.求证:四边形EGFH是平行四边形.
如图,在?ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E、F,GH过点O,与AB,CD分别相交于点G、H,连接EG、FG、FH、EH.求证:四边形EGFH是平行四边形.
19.下面四个手机应用图标中,属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
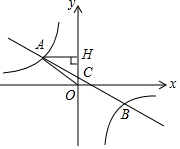 在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、第四象限内的A,B两点,与y轴交于C点,过A作AH⊥y轴,垂足为H,AH=4,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).
在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、第四象限内的A,B两点,与y轴交于C点,过A作AH⊥y轴,垂足为H,AH=4,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).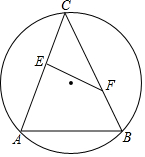 如图,点E,F分别在线段AC,BC上运动(不与端点重合),而且CE=BF,O是△ABC的外心,证明C,E,O,F四点共圆.
如图,点E,F分别在线段AC,BC上运动(不与端点重合),而且CE=BF,O是△ABC的外心,证明C,E,O,F四点共圆.