题目内容
17. (1)【阅读理解】
(1)【阅读理解】“|a|”的几何意义是:数a在数轴上对应的点到原点的距离.所以,“|a|≤2”可理解为:数a在数轴上对应的点到原点的距离不大于2;则:
①“|a|>2”可理解为:表示数a在数轴上对应的点到原点的距离大于2;
②请列举3个不同的数a,使不等式|a|≤2成立.列举的a的值是-1、0、1.
我们定义:形如“|x|≤m”、“|x|≥m”、“|x|>m”、“|x|<m”(m为非负数)
的不等式称为绝对值不等式.能使一个绝对值不等式成立的所有未知数的值称为这个绝对值不等式的解集.
(2)【理解运用】
根据绝对值的几何意义可以解一些绝对值不等式:
由图1可得出;绝对值不等式|x|≤3的解集是-3≤x≤3
由图2可得出:绝对值不等式|x|>4的解集是x<-4或x>4
那么,①不等式|x|<5的解集是-5<x<5;②不等式|$\frac{1}{2}$x|≥3的解集是x≥6或x≤-6;
(3)【灵活运用】
①不等式|x|<5的解集是-5<x<5;
②不等式|-$\frac{1}{200}$x+0.02|≤0.01的整数解是2,3,4,5,6.
分析 (1)根据绝对值的几何意义,结合题意进行解答;
(2)根据绝对值的几何意义,进行一元一次不等式的求解;
(3)根据(1)(2)的理解,进行绝对值的化简,然后解一元一次不等式.
解答 解:(1)①表示数a在数轴上对应的点到原点的距离大于2;
②∵|a|≤2,
∴-2≤a≤2,
则满足题意的a值为:-1,0,1;
(2)①不等式|x|<5的解集是-5<x<5;
②进行绝对值的化简得:$\frac{1}{2}$x≥3或$\frac{1}{2}$x≤-3,
解得:x≥6或x≤-6;
(3)①不等式|x|<5的解集是-5<x<5;
②进行绝对值的化简得:-0.01≤-$\frac{1}{200}$x+0.02≤0.01,
解得:2≤x≤6,
则不等式的整数解为:2,3,4,5,6.
故答案为:-1,0,1;-5<x<5;x≥6或x≤-6;2,3,4,5,6.
点评 本题考查了一元一次不等式的应用,解答本题的关键读懂题意以及掌握绝对值的几何意义和化简.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 矩形 | D. | 五角星 |
5. 如图(1)∠A与∠AEF是同旁内角;(2)∠BED与∠CFG是同位角;(3)∠AFE与∠BEF是内错角;(4)∠A与∠CFE是同位角,以上说法中,正确的是( )
如图(1)∠A与∠AEF是同旁内角;(2)∠BED与∠CFG是同位角;(3)∠AFE与∠BEF是内错角;(4)∠A与∠CFE是同位角,以上说法中,正确的是( )
 如图(1)∠A与∠AEF是同旁内角;(2)∠BED与∠CFG是同位角;(3)∠AFE与∠BEF是内错角;(4)∠A与∠CFE是同位角,以上说法中,正确的是( )
如图(1)∠A与∠AEF是同旁内角;(2)∠BED与∠CFG是同位角;(3)∠AFE与∠BEF是内错角;(4)∠A与∠CFE是同位角,以上说法中,正确的是( )| A. | (1)(2) | B. | (2)(3) | C. | (1)(3)(4) | D. | (1)(2)(3)(4) |
2.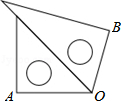 一副三角板如图所示放置,则∠AOB=( )
一副三角板如图所示放置,则∠AOB=( )
 一副三角板如图所示放置,则∠AOB=( )
一副三角板如图所示放置,则∠AOB=( )| A. | 60° | B. | 75° | C. | 105° | D. | 180° |
9.一元二次方程x(x-4)=4-x的根是( )
| A. | -1 | B. | 4 | C. | 1和4 | D. | -1和4 |
6.点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=$\frac{-2}{x}$的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )
| A. | y2<y1<y3 | B. | y1<y2<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |