题目内容
如图,四边形ABCD是正方形,点G是BC边上 任意一点,DE⊥AG于E,BF∥DE,交AG于F.
任意一点,DE⊥AG于E,BF∥DE,交AG于F.
(1)求证:AF-BF=EF;
(2)将△ABF绕点A逆时针旋转,使得AB与AD重合,记此时点F的对应点为点F′,若正方形边长为3 ,求点F′与旋转前的图中点E之间的距离.
,求点F′与旋转前的图中点E之间的距离.
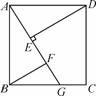
解:(1)证明:如图正方形ABCD中,AB=AD,∠2+∠3=90°.
∵DE⊥AG,∴∠AED=90°,∴∠1+∠3=90°,∴∠1=∠2.
又 ∵BF∥DE,∴∠AFB=∠AED=90°.
∵BF∥DE,∴∠AFB=∠AED=90°.
在△AED和△BFA中,

∴△AED≌△BFA.(4分)∴BF=AE.
∵AF-AE=EF,∴AF-BF=EF.(6分)
(2)如图,根据题意知:∠ FAF′=90°,
FAF′=90°,
DE=AF′=AF,
∴可判断四边形AEDF′为矩形,(10分)
∴EF′=AD=3.(12分)

练习册系列答案
相关题目
 B.
B.  C.
C. 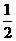 D.
D. 

 最大?最大面积是多少?
最大?最大面积是多少? 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值 ]
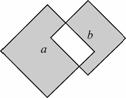
]
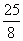 cm B.
cm B.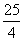 cm C.
cm C.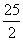 cm D.8
cm D.8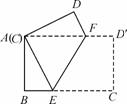
 的结果为( )
的结果为( ) .无解
.无解 知一个底面为菱形的直棱柱,
知一个底面为菱形的直棱柱, 高为10 cm,体积为150 cm3,则这个棱柱的下底面积为______cm2;若该棱柱侧面展开图的面积为200 cm2,记底面菱形的顶点依次为A,B,C,D,AE是BC边上的高,则CE的长为______cm.
高为10 cm,体积为150 cm3,则这个棱柱的下底面积为______cm2;若该棱柱侧面展开图的面积为200 cm2,记底面菱形的顶点依次为A,B,C,D,AE是BC边上的高,则CE的长为______cm.