Question

1．如图△ABC中，AB=AC，P是△ABC外一点，且∠APB=90°-$\frac{1}{2}$∠BAC．
（1）求证：PA是△PBC的外角∠BPD的平分线；
（2）作AE⊥PB于E，求证：PC+PE=BE；
（3）若△ABC是等边三角形，求证：PA+PC=PB．

Answer 1

分析 （1）只要证明A、B、C、P四点共圆即可得到∠2=∠1，∠APD=∠ABC，而∠ABC=∠1是很容易证明的．
（2）作AM⊥PD垂足为M，只要证明PE=PM，CM=BE即可解决问题．
（3）如图3中，在PB上取一点E使得AE=AP，先利用四点共圆证明△AEP是等边三角形，再证明△BAE≌△CAP得到BE=PC，利用PB=PE+BE即可证明．

解答 （1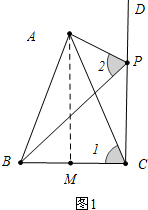）证明：如图1中，作AM⊥BC垂足为M，
∵AB=AC，AM⊥BC，
∴∠BAM=∠CAM=$\frac{1}{2}$∠BAC，∠AMC=90°，∠ABC=∠1，
∴∠1=90°-$∠CAM=90°-\frac{1}{2}∠BAC$，
∵$∠2=90°-\frac{1}{2}∠BAC$，
∴∠1=∠2，
∴A、B、C、P四点共圆，
∴∠APD=∠ABC=∠1，
∴∠2=∠APD，
∴AP平分∠BPD．
（2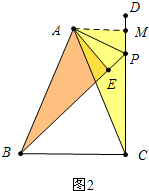）证明：在图2中，作AM⊥CD垂足为M，
∵∠APE=∠APD（已证），AE⊥PB，AM⊥PD，
∴AE=AM，∠AEB=∠AMC=90°
在RT△ABE和RT△ACM中，
$\left\{\begin{array}{l}{AB=AC}\\{AE=AM}\end{array}\right.$，
∴△ABE≌△ACM，
∴BE=CM，
在RT△APE和RT△APM中，
$\left\{\begin{array}{l}{AP=AP}\\{AE=AM}\end{array}\right.$，
∴△APE≌△APM，
∴PE=PM，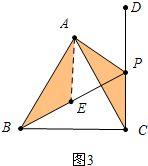
∴PC+PE=PC+PM=CM=BE．
（3）如图3中，在PB上取一点E使得AE=AP，
∵△ABC是等边三角形，
∴∠ABC=ACB=∠BAC=60°
由（1）可知ABCP四点共圆，
∴∠APB=∠ACB=60°，
∴△AEP是等边三角形，
∴∠EAP=∠BAC=60°，PA=PE=AE，
∴∠BAE=∠CAP，
在△BAE和△CAP中，
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAP}\\{AE=AP}\end{array}\right.$，
∴△BAE≌△CAP，
∴BE=PC，
∴PB=BE+PE=PC+PA．

点评 本题考查等腰三角形的性质、等边三角形的判定和性质、全等三角形的判定和性质、四点共圆等知识，通过添加辅助线构造全等三角形是解决问题的关键．