题目内容
2.如图,⊙O是△ABC的外接圆,直线DE是⊙O的切线,点A为切点,DE∥BC.(1)如图1,求证:AB=AC;
(2)如图2,点P是弧AB上一动点,连接PA,PB,作PF⊥PB,PF交⊙O于点F,求证:∠BAC=2∠APF;
(3)如图3,在(2)的条件下,连接PC,PA=2$\sqrt{5}$,PB=5$\sqrt{2}$,PC=7$\sqrt{2}$,求线段PF的长.
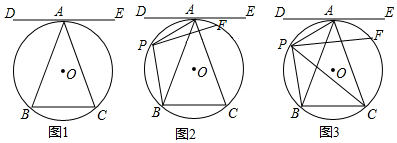
分析 (1)如图1中,连接OA,延长AO交BC于H.只要证明AH垂直平分线段BC即可.
(2)如图2中,连接OA、BF.首先证明BF是直径,可得∠1=∠3,再证明OA平分∠BAC即可解决问题.
(3)如图3中,连接AF、CF、BF、OA延长OA交BC于H,在AB上取一点K,使得∠BPK=∠APC,作BM⊥PC于M.首先证明托勒密定理:PB•AC+PA•BC=PC•AB,推出BC:AB=$\sqrt{2}$:$\sqrt{5}$,BC=$\sqrt{2}$k,AB=AC=$\sqrt{5}$k,⊙O的半径为r.在Rt△ABH中,AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=$\frac{3\sqrt{2}}{2}$k,在Rt△OBH中,∵OB2=OH2+BH2,得到r2=($\frac{\sqrt{2}}{2}$k)2+($\frac{3\sqrt{2}}{2}$k-r)2,推出r=$\frac{5\sqrt{2}}{6}$k,在Rt△FBC中,sin∠BFC=$\frac{BC}{BF}$=$\frac{\sqrt{2}k}{\frac{5\sqrt{2}}{3}k}$=$\frac{3}{4}$,推出cos∠BFC=$\frac{4}{5}$,在Rt△PBM中,PB=5$\sqrt{2}$,由∠BPC=∠BFC,推出PM=PB•cos∠PBC=$\frac{4}{5}$×5$\sqrt{2}$=4$\sqrt{2}$,BM=PB•sin∠BPC=5$\sqrt{2}$×$\frac{3}{5}$=3$\sqrt{2}$,CM=PC=PM=3$\sqrt{2}$,推出BM=CM=3$\sqrt{2}$,推出BC=$\sqrt{2}$CM=6,可得方程$\sqrt{2}$k=6,求得k=3$\sqrt{2}$,求出半径即可解决问题.
解答 (1)证明:如图1中,连接OA,延长AO交BC于H.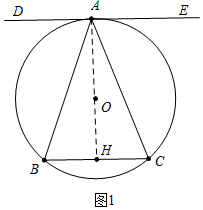
∵DE是切线,
∴OA⊥DE,
∵DE∥BC,
∴AH⊥BC,
∴BH=CH,
∴AB=AC.
(2)证明:如图2中,连接OA、BF.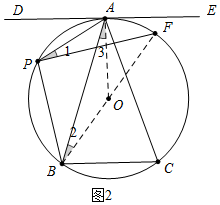
∵BP⊥PF,
∴∠BPF=90°,
∴BF是直径,
∵OB=OA,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
由(1)可知,AB=AC,AO⊥BC,
∴OA平分∠BAC,
∴∠BAC=2∠3=2∠1,
∴∠BAC=2∠APF.
(3)解:如图3中,连接AF、CF、BF、OA延长OA交BC于H,在AB上取一点K,使得∠BPK=∠APC,作BM⊥PC于M.
∵∠BPK=∠APC,∠AFP=∠PBK,
∴△APC∽△KPB,
∴PB•AC=BK•PC ①
∵∠APK=∠CPB,∠PAK=∠PCB,
∴△APK∽△CPB,
∴PA•BC=PC•AK ②,
①+②得PB•AC+PA•BC=PC•AB,
∵AB=AC,
∴$\frac{BC}{AB}$=$\frac{7\sqrt{2}-5\sqrt{2}}{2\sqrt{5}}$=$\frac{\sqrt{2}}{\sqrt{5}}$,设,BC=$\sqrt{2}$k,AB=AC=$\sqrt{5}$k,⊙O的半径为r.
在Rt△ABH中,AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=$\frac{3\sqrt{2}}{2}$k,
在Rt△OBH中,∵OB2=OH2+BH2,
∴r2=($\frac{\sqrt{2}}{2}$k)2+($\frac{3\sqrt{2}}{2}$k-r)2,
∴r=$\frac{5\sqrt{2}}{6}$k,
在Rt△FBC中,sin∠BFC=$\frac{BC}{BF}$=$\frac{\sqrt{2}k}{\frac{5\sqrt{2}}{3}k}$=$\frac{3}{4}$,
∴cos∠BFC=$\frac{4}{5}$,
在Rt△PBM中,∵PB=5$\sqrt{2}$,∠BPC=∠BFC,
∴PM=PB•cos∠PBC=$\frac{4}{5}$×5$\sqrt{2}$=4$\sqrt{2}$,BM=PB•sin∠BPC=5$\sqrt{2}$×$\frac{3}{5}$=3$\sqrt{2}$,
∴CM=PC=PM=3$\sqrt{2}$,
∴BM=CM=3$\sqrt{2}$,
∴BC=$\sqrt{2}$CM=6,
∴$\sqrt{2}$k=6,
∴k=3$\sqrt{2}$,
∴r=$\frac{5\sqrt{2}}{6}$×$3\sqrt{2}$=5,
在Rt△PBF中,PF=$\sqrt{B{F}^{2}-P{B}^{2}}$=$\sqrt{1{0}^{2}-(5\sqrt{2})^{2}}$=5$\sqrt{2}$.
点评 本题考查圆综合题、切线的性质、相似三角形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是证明了托勒密定理:PB•AC+PA•BC=PC•AB,学会利用参数解决问题,题目比较难,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案
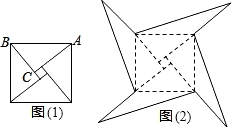 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )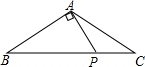 如图,在△ABC中,AB=AC,∠BAC=120°,P是BC上一点,且∠BAP=90°,PC=4cm,则BC的长为12cm.
如图,在△ABC中,AB=AC,∠BAC=120°,P是BC上一点,且∠BAP=90°,PC=4cm,则BC的长为12cm.