题目内容
15．已知扇形的圆心角为60°，它的弧长为2πcm，则扇形的半径是6cm，扇形的面积是6πcm2．分析 设扇形的半径为r，根据弧长公式可求出r的值，再由扇形的面积公式即可得出结论．
解答 解：设扇形的半径为r，
∵扇形的圆心角为60°，它的弧长为2πcm，
∴$\frac{60πr}{180}$=2π，解得r=6（cm），
∴S扇形=$\frac{1}{2}$×2π×6=6π．
故答案为：6，6π．
点评 本题考查的是扇形面积的计算，熟记扇形的面积公式是解答此题的关键．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
5．
已知有理数a、b在数轴上表示的点如图所示，则下列式子中正确的是（ ）
已知有理数a、b在数轴上表示的点如图所示，则下列式子中正确的是（ ）| A． | a+b＞0 | B． | a-b＜0 | C． | ab＞0 | D． | $\frac{a}{b}＜0$ |
6．
如图，Rt△ABC中，∠ACB=90°，∠B=30°，AC=2，将△ABC绕点C逆时针旋转至△A′B′C，使得点A′恰好落在AB上，A′B′与BC交于点D，则△A′CD的面积为（ ）
如图，Rt△ABC中，∠ACB=90°，∠B=30°，AC=2，将△ABC绕点C逆时针旋转至△A′B′C，使得点A′恰好落在AB上，A′B′与BC交于点D，则△A′CD的面积为（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | 3$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | 2$\sqrt{3}$ |
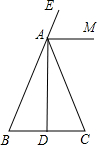如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线．
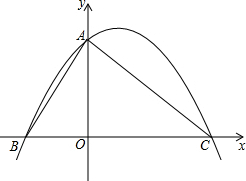将直角边长为4的等腰Rt△AOC放在如图所示的平面直角坐标系中，点O为坐标原点，点C、A分别在x、y轴的正半轴上，一条抛物线经过点A、C及点B（-2，0）． 
共有5个正三角形，从位置来看，下图中（ ）是由如图平移得到的．
