题目内容
11. 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|. 利用数形结合思想回答下列问题:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|. 利用数形结合思想回答下列问题:(1)数轴上表示x和-1的两点之间的距离表示为|x+1|或|x-(-1)|;
(2)若x表示一个有理数,且-4<x<2,则|x-2|-|x+4|=-2x-6;
(3)利用数轴求解,|x+2|+|x+4|的最小值是2,并写出此时x的整数值-2,-3,-4.
分析 (1)根据两点之间的距离的定义解答即可;
(3)由-4<x<2得,|x-2|-|x+4|化简解答即可;
(3)由|x+2|+|x+4|实际是-4与-2的距离,得出即可.
解答 解:(1)数轴上表示x和-1的两点之间的距离表示为:|x+1|或|x-(-1)|;
(2)因为-4<x<2,
所以|x-2|-|x+4|=-2x-6;
(3)|x+2|+|x+4|的最小值是2;此时x的整数值是-2,-3,-4;
故答案为:|x+1|或|x-(-1)|;-2x-6;2;-2,-3,-4
点评 本题主要考查的是数的绝对值,首先要牢记绝对值的定义以及几何和代数的意义.

练习册系列答案
相关题目
6.已知代数式x+2y的值是3,则代数式2x+4y+2010的值是( )
| A. | 2013 | B. | 2014 | C. | 2015 | D. | 2016 |
4.若-6xayzb与9x3ycz2是同类项,则a、b、c的值分别是( )
| A. | a=1,b=2,c=3 | B. | a=3,b=1,c=2 | C. | a=3,b=2,c=1 | D. | 以上都不对 |
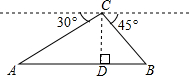 如图,从坡顶C处测得地面A、B两点的俯角分别为30°、45°,如果此时C出的高度CD为150米,且点A、D、B在同一直线上,则AB两点间距离是(150$\sqrt{3}$+150)米.
如图,从坡顶C处测得地面A、B两点的俯角分别为30°、45°,如果此时C出的高度CD为150米,且点A、D、B在同一直线上,则AB两点间距离是(150$\sqrt{3}$+150)米. 如图,在?ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.
如图,在?ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.