题目内容
11.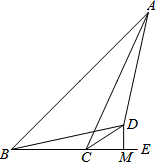 已知:如图,点B、C、E三点在同一条直线上,CD平分∠ACE,DB=DA,DM⊥BE于M.
已知:如图,点B、C、E三点在同一条直线上,CD平分∠ACE,DB=DA,DM⊥BE于M.(1)求证:AC=BM+CM;
(2)若AC=2,BC=1,求CM的长.
分析 (1)作DN⊥AC于N,易证Rt△DCN≌Rt△DCM,可得CN=CM,进而可以证明Rt△ADN≌Rt△BDM,可得AN=BM,即可解题;
(2)利用(1)中的结论变形得出答案即可.
解答 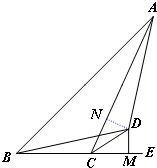 (1)证明:作DN⊥AC于N,
(1)证明:作DN⊥AC于N,
∵CD平分∠ACE,DM⊥BE
∴DN=DM,
在Rt△DCN和Rt△DCM中,
$\left\{\begin{array}{l}CD=CD\\ DN=DM\end{array}\right.$
∴Rt△DCN≌Rt△DCM(HL),
∴CN=CM,
在Rt△ADN和Rt△BDM中,
$\left\{\begin{array}{l}AD=BD\\ DN=DM\end{array}\right.$
∴Rt△ADN≌Rt△BDM(HL),
∴AN=BM,
∵AC=AN+CN,
∴AC=BM+CM.
(2)解:∵AN=AC-CN,BM=BC+CM,
∴AC-CN=BC+CM,
∴AC-CM=BC+CM,
∴2CM=AC-BC,
∵AC=2,BC=1,
∴CM=0.5.
点评 本题考查了直角三角形全等的判定,考查了直角三角形对应边相等的性质,本题中求证CN=CM,AN=BM是解题的关键.

练习册系列答案
相关题目
1.化简-[-(x-y)]-[-(x+y)]可得( )
| A. | 2x | B. | 2x+2y | C. | 2y | D. | 2x-2y |
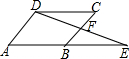 如图,AB∥CD,AD∥BC,E为AB延长线上一点,连结DE交BC于点F,在不添加任何辅助线的情况下,请补充一个条件,使△BEF≌△CDF,你补充的条件是DC=BE(写一个即可).
如图,AB∥CD,AD∥BC,E为AB延长线上一点,连结DE交BC于点F,在不添加任何辅助线的情况下,请补充一个条件,使△BEF≌△CDF,你补充的条件是DC=BE(写一个即可).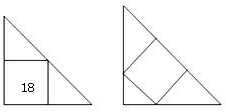 在一个给定的等腰直用三角形中作内接正方形,可以有如图所示的2种办法,如果其中一种得出的正方形的面积为18,那么另一种方法得到的正方形面积为( )
在一个给定的等腰直用三角形中作内接正方形,可以有如图所示的2种办法,如果其中一种得出的正方形的面积为18,那么另一种方法得到的正方形面积为( ) 如图,在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,点D,E分别在AC,BC边上,且∠DOE=90°,DE交OC于P,下列结论正确的共有( )
如图,在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,点D,E分别在AC,BC边上,且∠DOE=90°,DE交OC于P,下列结论正确的共有( )