题目内容
19.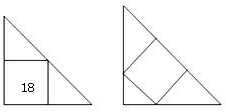 在一个给定的等腰直用三角形中作内接正方形,可以有如图所示的2种办法,如果其中一种得出的正方形的面积为18,那么另一种方法得到的正方形面积为( )
在一个给定的等腰直用三角形中作内接正方形,可以有如图所示的2种办法,如果其中一种得出的正方形的面积为18,那么另一种方法得到的正方形面积为( )| A. | 18 | B. | 19 | C. | 16 | D. | 17 |
分析 如图1,根据等腰直角三角形的性质得到∠A=∠C=45°,由正方形的性质得到∠FDB=∠FEC=90°,于是得到AD=BD=DF=BE=CE=3$\sqrt{2}$,求得AC=12,如图2,根据已知条件得到△ADG与△CEF是等腰直角三角形,得到CF=GF=AG=$\frac{1}{3}$AC=4,于是求得结论.
解答 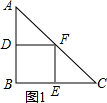 解:如图1,∵△ABC是等腰直角三角形,
解:如图1,∵△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∵四边形DBEF是正方形,
∴∠FDB=∠FEC=90°,
∴AD=BD=DF=BE=CE=3$\sqrt{2}$,
∴AB=BC=6$\sqrt{2}$,
∴AC=12,
如图2,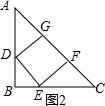
∵四边形DEFG是正方形,
∴∠DGF=∠EFG=90°,
∴∠AGD=∠CFE=90°,
∴△ADG与△CEF是等腰直角三角形,
∴CF=GF=AG=$\frac{1}{3}$AC=4,
∴S正方形DEFG=16,
故选C.
点评 本题考查了正方形的性质,等腰直角三角形的性质和判定,证得△ADG与△CEF是等腰直角三角形是解题的关键.

练习册系列答案
相关题目
9.下列各数中,属于无理数的是( )
| A. | $\root{3}{8}$ | B. | $\sqrt{8}$ | C. | $\frac{22}{7}$ | D. | 3.1415926 |
10.当1<a<2时,式子$\sqrt{(a-2)^{2}}$+|1-a|的值为( )
| A. | 3-2a | B. | 2a-3 | C. | -1 | D. | 1 |
14.已知cosB=$\frac{{\sqrt{3}}}{2}$,则∠B的值为( )
| A. | 30° | B. | 60° | C. | 45° | D. | 90° |
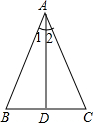 如图,在△ABC中,AB=AC,AD⊥BC于D.求证:BD=CD,∠1=∠2.
如图,在△ABC中,AB=AC,AD⊥BC于D.求证:BD=CD,∠1=∠2.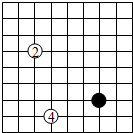 如图,围棋棋盘放置在某个平面直角坐标系内,白棋②的坐标为(-7,-4),白棋④的坐标为(-6,-8),那么黑棋的坐标应该是(-3,-7).
如图,围棋棋盘放置在某个平面直角坐标系内,白棋②的坐标为(-7,-4),白棋④的坐标为(-6,-8),那么黑棋的坐标应该是(-3,-7).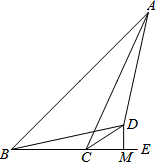 已知:如图,点B、C、E三点在同一条直线上,CD平分∠ACE,DB=DA,DM⊥BE于M.
已知:如图,点B、C、E三点在同一条直线上,CD平分∠ACE,DB=DA,DM⊥BE于M.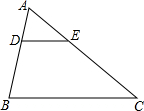 如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为9.
如图,在△ABC中,DE∥BC,AD=2,DB=4,DE=3,则BC的长为9.