题目内容
13.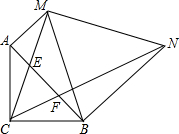 如图,等腰直角△ACB,CA=CB,∠ACB=90°,∠ECF=45°,点E、F在AB上,AM⊥AB,BN⊥AB,AM、BN分别交直线CE、CF于M、N,若AM=2,BN=5,则MN的长为$\sqrt{11}$.
如图,等腰直角△ACB,CA=CB,∠ACB=90°,∠ECF=45°,点E、F在AB上,AM⊥AB,BN⊥AB,AM、BN分别交直线CE、CF于M、N,若AM=2,BN=5,则MN的长为$\sqrt{11}$.
分析 根据等腰直角三角形的性质得到∠6=45°,推出∠5=∠ACF,证得△ACF∽△BCE,根据相似三角形的性质得到AC•BC=AF•BE,根据已知条件得到∠CAM=∠CBN=135°,推出△ACM∽△CBN,根据相似三角形的性质得到AC•BC=AM•BN=10,过M作MG⊥BN于G,则四边形ABGM是矩形,根据矩形的性质得到MG=AB,BG=AM=2,由于AB2=AC2+BC2=2AC2=2AC•BC=20,得到MG2=20,根据勾股定理即可得到结论.
解答 解:∵CA=CB,∠ACB=90°,
∴∠6=45°,
∵∠5=∠6+∠1=45°+∠1,∠ACF=∠1+∠2=∠1+45°,
∴∠5=∠ACF,
∵∠6=∠ABC=45°,
∴△ACF∽△BCE,
∴$\frac{AC}{BE}=\frac{AF}{BC}$,
∴AC•BC=AF•BE,
∵AM⊥AB,BN⊥AB,
∴∠ABN=90°,
∴∠CAM=∠CBN=135°,
∵∠2=45°,
∴∠1+∠3=45°,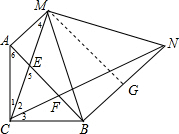
∵∠1+∠4=45°,
∴∠1=∠4,
∴△ACM∽△CBN,
∴$\frac{AC}{BN}=\frac{AM}{BC}$,
∴AC•BC=AM•BN=10,
过M作MG⊥BN于G,
则四边形ABGM是矩形,
∴MG=AB,BG=AM=2,
∴NG=3,
∵AB2=AC2+BC2=2AC2=2AC•BC=20,
∴MG2=20,
∴MN=$\sqrt{A{B}^{2}-G{N}^{2}}$=$\sqrt{11}$.
故答案为:$\sqrt{11}$.
点评 本题考查了相似三角形的判定和性质,勾股定理,矩形的判定和性质,等腰直角三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
3.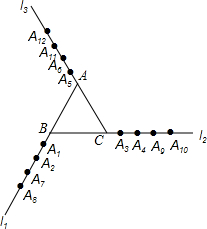 如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
 如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )
如图,将△ABC的各边分别延长,得到直线l1、l2、l3,从l1开始分别在各直线上标记点A1,A2,A3,A4,A5,A6,…,按此规律,则点A2013( )| A. | 在直线l1上 | B. | 在直线l2上 | ||
| C. | 在直线l3上 | D. | 不能确定在哪条直线上 |
1.(-3)100×($-\frac{1}{3}$)100等于( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | 1 |
 已知等腰△DEF中,DE=DF,求作△DEF的外接圆.(尺规作图,保留作图痕迹)
已知等腰△DEF中,DE=DF,求作△DEF的外接圆.(尺规作图,保留作图痕迹)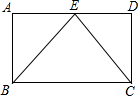 如图所示,在?ABCD中,E为AD的中点,△CBE是等边三角形,求证:?ABCD是矩形.
如图所示,在?ABCD中,E为AD的中点,△CBE是等边三角形,求证:?ABCD是矩形.