题目内容
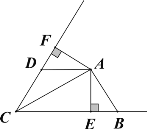
【题目】如图，矩形ABCD 和正方形ECGF，其中E、H分别为AD、BC中点，连结AF、HG、AH.
（1）求证：
；
（2）求证：
；
【答案】（1）详见解析；（2）详见解析.
【解析】
（1）根据题意可先证明四边形AHCE为平行四边形，再根据正方形的性质得到∴
，
，故可证明四边形AHGF是平行四边形，即可求解；
（2）根据四边形AHGF是平行四边形，得
，根据四边形ABCD是矩形，可得 
，再根据平角的性质及等量替换即可证明.
（1）证明：∵四边形ABCD是矩形，且E、H分别为AD、BC的中点，
∴
，
，
∴四边形AHCE为平行四边形，
∴
，
，
又∵四边形ECGF为正方形，
∴
，
，
∴，，
∴四边形AHGF是平行四边形，
∴；
（2）证明：∵四边形AHGF是平行四边形，
∴，
∵四边形ABCD是矩形，
∴
，
∴，
又∵
，
∴
；
练习册系列答案
名校课堂系列答案
相关题目
