题目内容
 如图,△ABC,点D、E、F分别在三边上,E是AC的中点,BC=3DC,AD、BE、CF交于一点G,S△GEC=2cm2,S△GBD=
如图,△ABC,点D、E、F分别在三边上,E是AC的中点,BC=3DC,AD、BE、CF交于一点G,S△GEC=2cm2,S△GBD=| 16 |
| 3 |
考点:三角形的面积
专题:
分析:根据等底等高的三角形的面积相等求出△AGE的面积,再根据等高的三角形的面积的比等于底边的比求出△CDG的面积,然后求出△ACD的面积,最后根据等高的三角形的面积的比等于底边的比列式计算即可得解.
解答:解:∵E是AC的中点,
∴S△AGE=S△GEC=2cm2,
∵BC=3DC,
∴BD=2DC,
∴S△CDG=
S△GBD=
×
=
cm2,
∴S△ACD=S△AGE+S△GEC+S△CDG=2+2+
=
cm2,
∵BC=3DC,
∴S△ABC=3S△ACD=3×
=20cm2.
故答案为:20.
∴S△AGE=S△GEC=2cm2,
∵BC=3DC,
∴BD=2DC,
∴S△CDG=
| 1 |
| 2 |
| 1 |
| 2 |
| 16 |
| 3 |
| 8 |
| 3 |
∴S△ACD=S△AGE+S△GEC+S△CDG=2+2+
| 8 |
| 3 |
| 20 |
| 3 |
∵BC=3DC,
∴S△ABC=3S△ACD=3×
| 20 |
| 3 |
故答案为:20.
点评:本题考查了三角形的面积,主要利用了等底等高的三角形的面积相等,等高的三角形的面积的比等于底边的比,需熟记.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,两个圆盘中,指针落在每一个数上的机会均等,则指针同时落在偶数上的概率是( )
如图,两个圆盘中,指针落在每一个数上的机会均等,则指针同时落在偶数上的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
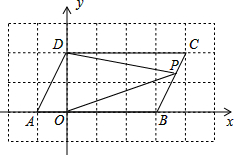 如图,在直角坐标系xOy中,A(-1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.
如图,在直角坐标系xOy中,A(-1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC. 如图,△ABC≌△BAD,若AB=6、AC=4、BC=5,则AD的长为
如图,△ABC≌△BAD,若AB=6、AC=4、BC=5,则AD的长为 如图,已知点O是四边形ABCD内一点,且有OA=OB=OC,∠ABC=70°,则∠AOC=
如图,已知点O是四边形ABCD内一点,且有OA=OB=OC,∠ABC=70°,则∠AOC= 如图,BA=BC,EB∥AC,∠A=55°,则∠DBE的度数为
如图,BA=BC,EB∥AC,∠A=55°,则∠DBE的度数为