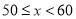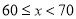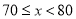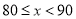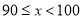题目内容
二次函数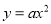 的图象一定过点( )
的图象一定过点( )
A. (0,0) B. (1,2) C. (—1,2) D. 以上都正确
A 【解析】根据二次函数的图象的性质可得, 二次函数的图象一定过点(0,0),故选A.下列四组线段中,不能组成比例线段的是( )
A. 
B. 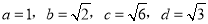
C. 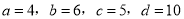
D. 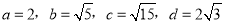
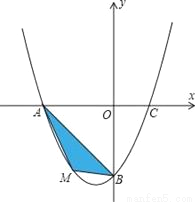
如图,在平面直角坐标系中,已知抛物线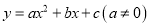 与x轴相交于
与x轴相交于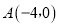 ,C两点
,C两点 与y轴相交于点B
与y轴相交于点B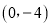 .
.
 a 0,
a 0, 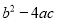
 填“
填“ ”或“
”或“ ”
” 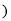 ;
;
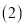 若该抛物线关于直线
若该抛物线关于直线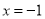 对称,求抛物线的函数表达式;
对称,求抛物线的函数表达式;
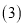 在
在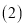 的条件下,若点M为第三象限内抛物线上一动点,点M的横坐标为
的条件下,若点M为第三象限内抛物线上一动点,点M的横坐标为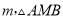 的面积为
的面积为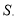 求S关于m的函数关系式,并求出S的最大值;
求S关于m的函数关系式,并求出S的最大值;
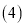 在
在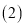 的条件下,若点P是抛物线上的动点,点Q是直线
的条件下,若点P是抛物线上的动点,点Q是直线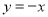 上的动点,判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
阅读材料:善于思考的小军在解方程组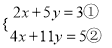 时,采用了一种“整体代换”的解法:
时,采用了一种“整体代换”的解法:
【解析】
将方程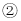 变形:
变形: 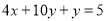 即
即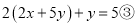
把方程 带入
带入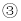 得:
得: 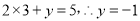
把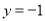 代入
代入 得
得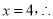 方程组的解为
方程组的解为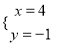 .
.
请你解决以下问题:
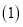 模仿小军的“整体代换”法解方程组
模仿小军的“整体代换”法解方程组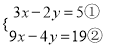
 已知
已知 满足方程组
满足方程组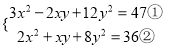 .
.
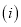 求
求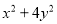 的值;
的值;
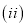 求
求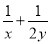 的值.
的值.
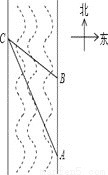
在2014年6月23日第十届保护韩江母亲河徒步节上,如图所示,某同学为了测得一段南北流向的河段的宽,在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西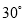 的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西
的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西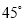 的方向上,请你根据以上数据,求这段河段的宽度
的方向上,请你根据以上数据,求这段河段的宽度 结果保留根号
结果保留根号
为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B两种型号的学习用品共1000件,已知A型学习用品的单价为20元,B型学习用品的单价为30元.
(1)若购买这批学习用品用了26000元,则购买A,B两种学习用品各多少件?
(2)若购买这批学习用品的钱不超过28000元,则最多购买B型学习用品多少件?
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案若(a+1)2+|b﹣2|=0,化简a(x2y+xy2)﹣b(x2y﹣xy2)的结果为( )
A.3x2y B.﹣3x2y+xy2 C.﹣3x2y+3xy2 D.3x2y﹣xy2
B 【解析】 试题分析:利用非负数的性质求出a与b的值,代入原式,去括号合并即可得到结果. 【解析】 ∵(a+1)2+|b﹣2|=0, ∴a+1=0,b﹣2=0,即a=﹣1,b=2, 则原式=﹣(x2y+xy2)﹣2(x2y﹣xy2)=﹣x2y﹣xy2﹣2x2y+2xy2=﹣3x2y+xy2. 故选B给出条件:①两条直线相交成直角;②两条直线互相垂直;③一条直线是另一直线的垂线,并且能否以上述任何一个为条件得出另外两个为内容的结论,正确的是( )
A. 能 B. 不能 C. 有的能有的不能 D. 无法确定
查看答案已知|3x|﹣y=0,|x|=1,则y的值等于( )
A. 3或﹣3 B. 11 C. -3 D. 3
查看答案现有四种说法:①-a表示负数; ②若|x|=-x,则x<0; ③绝对值最小的有理数是0;④3×102x2y是5次单项式;其中正确的是( )
A. ① B. ② C. ③ D. ④
查看答案在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐上,且点A(0,2),点C(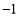 ,0),如图所示:抛物线
,0),如图所示:抛物线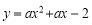 经过点B。
经过点B。
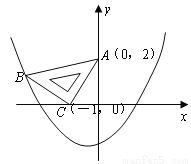
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
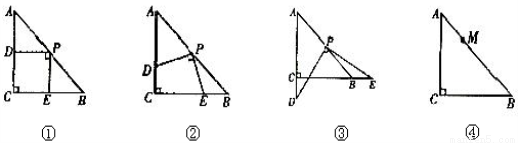
查看答案操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰三角形板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。图①,②,③是旋转三角板得到的图形中的3种情况。研究:
(1)三角板ABC绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合图②加以证明。
(2)三角板ABC绕点P旋转,△PBE是否能为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。(图④不用)
- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某工厂有煤 吨,计划每天用煤
吨,计划每天用煤 吨.实际每天节约用煤
吨.实际每天节约用煤 吨,那么这些煤可比原计划多用( ).
吨,那么这些煤可比原计划多用( ).
A. 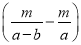 天 B.
天 B. 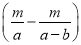 天 C.
天 C. 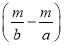 天 D.
天 D. 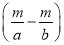 天
天
如果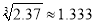 ,
, 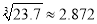 ,那么
,那么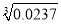 约等于( ).
约等于( ).
A. 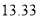 B.
B. 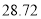 C.
C. 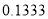 D.
D. 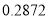
下列各组中.是同类项的是( ).
①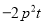 与
与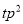 ;②
;②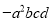 与
与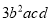 ;③
;③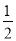 与
与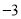 ;④
;④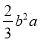 与
与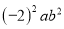 .
.
A. ①②③ B. ①③④ C. ②③④ D. ①②④
查看答案比较数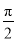 ,
, 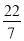 ,
, 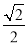 ,
, 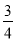 的共同点,它们都是( ).
的共同点,它们都是( ).
A. 分数 B. 有理数 C. 无理数 D. 正数
查看答案数轴上表示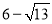 的点
的点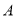 的位置应在( ).
的位置应在( ).
A. 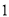 与
与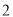 之间 B.
之间 B. 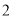 与
与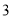 之间 C.
之间 C. 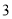 与
与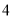 之间 D.
之间 D. 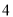 与
与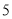 之间
之间
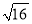 的平方根是 ( )
的平方根是 ( )
A. 4 B. 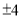 C.
C. 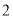 D.
D. 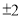
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
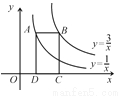
如图,点A在双曲线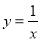 上,点B在双曲线
上,点B在双曲线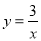 上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.
上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为__________.
如图所示,冰冰在墙上挂了一面镜子AB,调整好标杆CD,正好通过标杆顶部在镜子上边缘A处看到旗杆的顶端E的影子,已知AB=2m,CD=1.5m,BD=2m,BF=20m,则旗杆EF的高度为__________m。
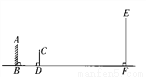
如图,在ΔABC中,∠ACB=90°,AC=7,BC=3,CM、CH 分别是中线和高,则SΔACM:SΔBCM = __________,SΔACH:SΔBCH = __________.
已知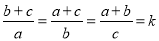 ,则抛物线
,则抛物线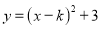 的顶点坐标为____________。
的顶点坐标为____________。
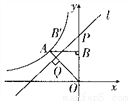
如图,反比例函数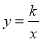 (k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
(k<0)的图象经过点A(-1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到了点B’在此反比例函数的图象上,则t的值是( )
A. 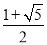 B.
B. 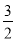 C.
C. 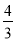 D.
D. 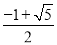
如图,E(-4,2),F(-1,-1),以O为位似中心,按比例尺1:2,把△EOF缩小,则点E的对应点E′的坐标为( ).
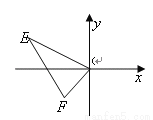
A. (2,-1)或(-2,1) B. (8,-4)或(-8,4) C. (2,-1) D. (8,-4)
查看答案 试题属性- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
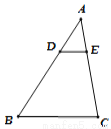
如图,在△ABC中, 若DE∥BC , 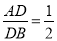 ,DE=4cm,则BC的长为 ( )
,DE=4cm,则BC的长为 ( )
A. 8cm B. 12cm C. 11cm D. 10cm
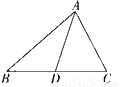
B 【解析】试题分析:因为=,所以,又因为DE∥BC,所以, 因为DE=4cm,所以,所以BC=12cm,故选:B.如图,下列各式能使ΔACB∽ΔDCA的是( )
A. 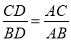 B.
B. 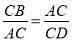 C.
C. 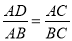 D.
D. 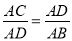
在同一平面直角坐标系中,一次函数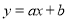
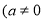 )和二次函数
)和二次函数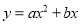
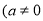 )的图象可能为( )
)的图象可能为( )
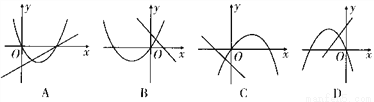
A. A B. B C. C D. D
查看答案抛物线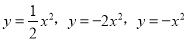 的图象开口最大的是( )
的图象开口最大的是( )
A. 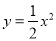 B.
B. 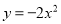 C.
C. 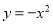 D. 无法确定
D. 无法确定
对于函数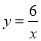 ,下列说法错误的是( )
,下列说法错误的是( )
A. 它的图象在第一、三象限
B. 它的图象既是轴对称图形又是中心对称图形
C. 当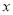 >0时,
>0时, 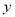 的值随
的值随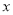 的增大而增大
的增大而增大
D. 当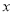 <0时,
<0时, 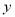 的值随
的值随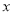 的增大而减小
的增大而减小
二次函数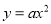 的图象一定过点( )
的图象一定过点( )
A. (0,0) B. (1,2) C. (—1,2) D. 以上都正确
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B两种型号的学习用品共1000件,已知A型学习用品的单价为20元,B型学习用品的单价为30元.
(1)若购买这批学习用品用了26000元,则购买A,B两种学习用品各多少件?
(2)若购买这批学习用品的钱不超过28000元,则最多购买B型学习用品多少件?
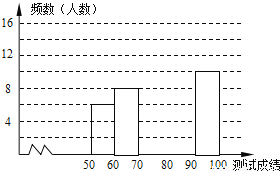
【解析】 (1)设购买A型学习用品x件,B型学习用品y件,由题意,得 ,解得:。 答:购买A型学习用品400件,B型学习用品600件。 (2)设最多可以购买B型产品a件,则A型产品(1000﹣a)件,由题意,得 20(1000﹣a)+30a≤28000, 解得:a≤800。 答:最多购买B型学习用品800件 【解析】 试题分析:(1)设购买A型学习...“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数 |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
| 14 |
第4组 |
| a |
第5组 |
| 10 |
请结合图表完成下列各题:
 求表中a的值;
求表中a的值;  频数分布直方图补充完整;
频数分布直方图补充完整;
 若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
 第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
如图,在平面直角坐标系中,一次函数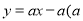 为常数
为常数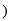 的图象与y轴相交于点A,与函数
的图象与y轴相交于点A,与函数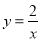 的图象相交于点
的图象相交于点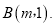
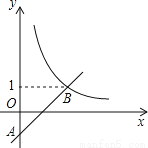
 求点B的坐标及一次函数的解析式;
求点B的坐标及一次函数的解析式;
 若点P在y轴上,且
若点P在y轴上,且 为直角三角形,请直接写出点P的坐标.
为直角三角形,请直接写出点P的坐标.
如图, 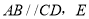 是CD上一点,BE交AD于点
是CD上一点,BE交AD于点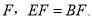 求证:
求证: 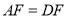 .
.
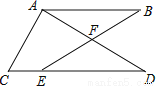
如图, 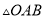 的底边经过
的底边经过 上的点C,且
上的点C,且 与OA、OB分别交于D、E两点.
与OA、OB分别交于D、E两点.
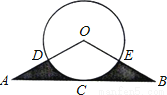
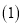 求证:AB是
求证:AB是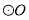 的切线;
的切线;
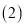 若D为OA的中点,阴影部分的面积为
若D为OA的中点,阴影部分的面积为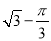 ,求
,求 的半径r.
的半径r.
化简: 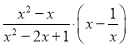
- 题型:解答题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
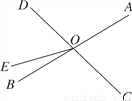
如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为________,∠BOE的补角为________;
(2)若∠AOC=75°,且∠BOE∶∠EOD=1∶4,求∠AOE的度数.
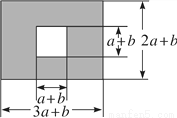
如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地,中间将修建一座边长为(a+b)米的正方形雕像,规划部门计划将余下部分进行绿化.
(1)试用含a,b的式子表示绿化部分的面积(结果要化简);
(2)若a=3,b=2,请求出绿化部分的面积.
计算:
(1)5x(2x2-3x+4);
(2)20172-2018×2016;
(3)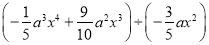 ;
;
(4)(a+b)(a-b)+(a+b)2-2a2.
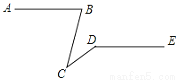
查看答案如图,已知AB∥DE,∠ABC=75°,∠CDE=150°,则∠BCD的度数为____.
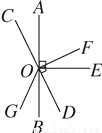
如图,直线AB与直线CD交于点O,OE⊥AB,∠DOF=90°,OB平分∠DOG,有下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的平分线;③与∠BOD相等的角有三个;④∠COG=∠AOB-2∠EOF.其中正确的结论是________(填序号).
已知(a-2b)2=9,(a+2b)2=25,则a2+4b2=________.
查看答案 试题属性- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下列各式中,与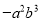 是同类项的是( )
是同类项的是( )
A. 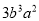 B.
B. 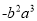 C.
C. 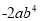 D.
D. 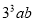
下列符合代数式的书写格式的是( )
A. -aab B. 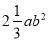 C.
C. 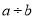 D.
D. 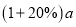
与-3的和为0的有理数是( )
A. -3 B. 3 C. 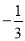 D.
D. 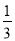
已知x≠1,(1+x)(1-x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4.
(1)根据以上式子计算:
①(1-2)×(1+2+22+23+24+25);
②2+22+23+…+2n(n为正整数);
③(x-1)(x99+x98+x97+…+x2+x+1).
(2)通过以上计算,请你进行下面的探索:
①(a-b)(a+b)=____________;
②(a-b)(a2+ab+b2)=____________;
③(a-b)(a3+a2b+ab2+b3)=____________.
查看答案一项工程,甲、乙两公司合做,12天可以完成,共需付工费102000元;如果甲、乙两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元。
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
查看答案如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
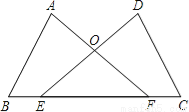
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


 人数
人数