题目内容
19.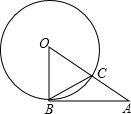 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BCA=115°,则∠A的度数为( )
如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BCA=115°,则∠A的度数为( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
分析 根据切线的性质求出∠OBA=90°,根据∠BCA=115°求出∠OCB=65°,根据等腰三角形性质求出∠OBC=∠OCB=65°,根据三角形内角和定理求出∠O,再根据三角形内角和定理求出即可.
解答 解:∵AB是⊙O的切线,B为切点,
∴∠OBA=90°,
∵∠BCA=115°,
∴∠OCB=180°-115°=65°,
∵OB=OC,
∴∠OBC=∠OCB=65°,
∴∠O=180°-∠OBC-∠OCB=50°,
∵∠OBA=90°,
∴∠A=180°-90°-50°=40°,
故选A.
点评 本题考查了切线的性质,三角形内角和定理,等腰三角形的性质的应用,能求出∠O和∠OBA的度数是解此题的关键.

练习册系列答案
相关题目
10.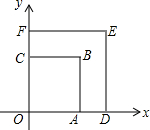 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
 如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )
如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,位似比为2:3,点B、E在第一象限,若点A的坐标为(1,0),则点E的坐标是( )| A. | ($\sqrt{2},0$) | B. | ($\frac{3}{2},\frac{3}{2}$) | C. | ($\sqrt{2},\sqrt{2}$) | D. | (2,2) |
14.若$\frac{2}{x-4}$有意义,则x的取值范围是( )
| A. | x>4 | B. | x≠4 | C. | x≥4 | D. | x<4 |
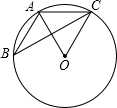 如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是60°.
如图,△ABC的顶点A,B,C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是60°.