题目内容
17. 如图,四边形ABCD内接于圆O,点E在对角线AC上.
如图,四边形ABCD内接于圆O,点E在对角线AC上.(1)若BC=DC,∠CBD=39°,求∠BCD的度数;
(2)若在AC上有一点E,且EC=BC=DC,求证:∠1=∠2.
分析 (1)根据BC=CD,得到$\widehat{BC}$=$\widehat{DC}$,求出∠BAD=78°,根据圆内接四边形的性质计算即可;
(2)根据等腰三角形的性质和三角形的外角的性质解答即可.
解答 解:(1)∵BC=CD,
∴$\widehat{BC}$=$\widehat{DC}$,
∴∠BAC=∠DAC=∠CBD=39°,
∴∠BAD=78°,
∵四边形ABCD为圆内接四边形,
∴∠BCD=102°;
(2)∵BC=CD,
∴∠CBD=∠CDB,又∠BAC=∠BDC,
∴∠CBD=∠BAE,
∴∠CEB=∠BAE+∠2,
∵CB=CE,
∴∠CBE=∠CEB,
∴∠BAE+∠2=∠CBD+∠1,
∴∠1=∠2.
点评 本题考查的是圆内接四边形的性质、圆周角定理的应用,掌握圆内接四边形的对角互补是解题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 如图,用一段长为20m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m.这个矩形的长、宽各是多少时,菜园面积最大?最大面积是多少?
如图,用一段长为20m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m.这个矩形的长、宽各是多少时,菜园面积最大?最大面积是多少? 请将数轴补全,然后把数-4,1,0,-|-1$\frac{1}{2}}$|,-(-5)表示在数轴上,并按从小到大的顺序,从左到右串个糖葫芦,把数填在“○”内.
请将数轴补全,然后把数-4,1,0,-|-1$\frac{1}{2}}$|,-(-5)表示在数轴上,并按从小到大的顺序,从左到右串个糖葫芦,把数填在“○”内.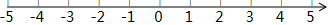 在数轴上表示下列各数,并用“<”号把它们按照从小到大的顺序排列.
在数轴上表示下列各数,并用“<”号把它们按照从小到大的顺序排列.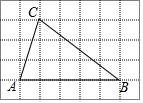 如图,已知△ABC,以AB为一边画△ABP,使之与△ABC全等(在方格纸中,画出所有符合条件的△ABP)
如图,已知△ABC,以AB为一边画△ABP,使之与△ABC全等(在方格纸中,画出所有符合条件的△ABP)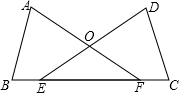 如图,点E、F在线段BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.求证:△ABF≌△DCE.
如图,点E、F在线段BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.求证:△ABF≌△DCE.