题目内容
7. 已知矩形OABC在直角坐标系中的位置如图,点B的坐标为(8,4).把矩形沿对角线OB折叠,使点A落在点D上,OD交CB于点E,过点E的双曲线y=$\frac{k}{x}$(x>0)交AB于F,求AF的长.
已知矩形OABC在直角坐标系中的位置如图,点B的坐标为(8,4).把矩形沿对角线OB折叠,使点A落在点D上,OD交CB于点E,过点E的双曲线y=$\frac{k}{x}$(x>0)交AB于F,求AF的长.
分析 先根据题意得出△OCE≌△BDE,故CE=DE设CE=DE=x,则BE=8-x,在△BDE中,根据勾股定理求出x的值,故可得出E点坐标,根据点E在双曲线y=$\frac{k}{x}$(x>0)上求出k的值,进而得出F点的坐标,由此可得出结论.
解答 解:∵△ODB由△OAB翻折而成,
∴BD=AB=OC,∠D=∠OAB=∠OCE,
在△OCE与△BDE中,
∵$\left\{\begin{array}{l}OC=BD\\∠OCE=∠D\\∠CEO=∠DEO\end{array}\right.$,
∴△OCE≌△BDE,
∴CE=DE.
设CE=DE=x,则BE=8-x,
△BDE中,由勾股定理得,x2+42=(8-x)2,
解得:x=3,
∴E(3,4),
∴K=3×4=12,
∴F(8,1.5),即AF=1.5.
点评 本题考查的是反比例函数综合题,先根据图形翻折变换的性质得出三角形全等,再由勾股定理列出方程求解是解答此题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
11.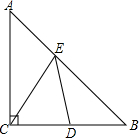 如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
 如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
15.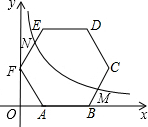 如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )
如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )
 如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )
如图,边长为4的正六边形ABCDEF的边AB在x轴上,顶点F在y轴上,点M是BC的中点,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过点M,且与正六边形交于另一点N,则点N的坐标是( )| A. | ($\frac{7}{4}\sqrt{3},4$) | B. | ($\frac{7}{4},4\sqrt{3}$) | C. | (2$\sqrt{2}-1,2\sqrt{6}+\sqrt{3}$) | D. | (2$\sqrt{2}+1,2\sqrt{6}-\sqrt{3}$) |
19.在△ABC中,如果∠A:∠B:∠C=1:1:2,那么△ABC的形状是( )
| A. | 锐角三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
16.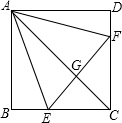 如图,已知在正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,给出下列结论:
如图,已知在正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,给出下列结论:
①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF.
其中结论正确的共有( )
 如图,已知在正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,给出下列结论:
如图,已知在正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,给出下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF.
其中结论正确的共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.下列根式中,是最简二次根式的为( )
| A. | $\sqrt{8a}$ | B. | $\sqrt{{a}^{2}+{b}^{2}}$ | C. | $\sqrt{0.1x}$ | D. | $\sqrt{{a}^{5}}$ |
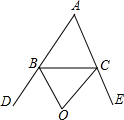 如图,OB、OC是△ABC的外角平分线,若∠A=50°,求∠BOC的度数.
如图,OB、OC是△ABC的外角平分线,若∠A=50°,求∠BOC的度数. 在平面直角坐标系中,点A(2,3)、B(3,1),O为坐标原点.
在平面直角坐标系中,点A(2,3)、B(3,1),O为坐标原点.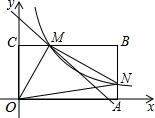 如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线y=-x+6交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线y=$\frac{k}{x}$(x>0)交边AB于点N.若△OAN的面积是4,求△OMN的面积.
如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线y=-x+6交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线y=$\frac{k}{x}$(x>0)交边AB于点N.若△OAN的面积是4,求△OMN的面积.