题目内容

17．如图所示，一次函数y=（m-1）x-3的图象分别与x轴、y轴的负半轴相交于A、B，则m的取值范围是m＜1．

分析 先一次函数y=（m-1）x-3的图象分别与x轴、y轴的负半轴相交于A、B，列出关于m的不等式，求出m的取值范围即可．

解答 解：因为一次函数y=（m-1）x-3的图象分别与x轴、y轴的负半轴相交于A、B，
可得：m-1＜0，
解得m＜1，
故答案为：m＜1．

点评 本题考查的是一次函数的图象与系数的关系，熟知一次函数y=kx+b（k≠0）中，当k＜0，b＜0时y随x的增大而减小，且函数与y轴负半轴相交是解答此题的关键．

练习册系列答案
相关题目
7．平面内的两条直线有相交和平行两种位置关系．
（1）如图1，若AB∥CD，点P在AB、CD外部，则有∠B=∠BOD，又因∠BOD是△POD的外角，故∠BOD=∠BPD+∠D．得∠BPD=∠B-∠D．将点P移到AB、CD内部，如图2，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何数量关系？请证明你的结论；
（2）在如图2中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图3，则∠BPD、∠B、∠D、∠BQD之间有何数量关系？（不需证明）；
（3）根据（2）的结论求如图4中∠A+∠B+∠C+∠D+∠E的度数．
8．已知某品牌遮阳伞如图①所示，图②是其剖面图，若AG同时平分∠BAC与∠EDF，且AB∥ED，则AC∥DF吗？请在下面括号内填写理由．
解：∵AB∥DE
∴∠DAB=∠GDE（两直线平行，同位角相等）
∵AG同时平分∠BAC与∠EDF（已知）
∴∠DAC=∠DAB，∠GDF=∠GDE（角平分线定义）
∴∠DAC=∠GDF（等量代换）
∴AC∥DF（同位角相等，两直线平行）
5．若二次函数y1=a1x2-1与二次函数y2=a2x2+3图象的形状完全相同，则a1与a2的关系为（　　）
A．a1=a2B．a1=-a2C．a1=±a2D．无法判断
12．计算：|-3|+（-$\frac{1}{3}$）0-$\root{3}{27}$．
2．若⊙O的半径为4，圆心O到直线l的距离为5，则直线l与⊙O的位置关系是（　　）
A．相交B．相切C．相离D．无法确定
9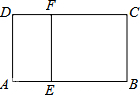．如图，矩形ABCD∽矩形ADFE，AE=1，AB=4，则AD=（　　）
A．2B．2.4C．2.5D．3
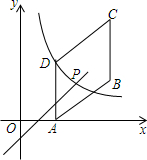6．如图，四边形ABCD是平行四边形，点A（1，0），B（3，1），C（3，3），反比例函数y=$\frac{m}{x}$（x＞0）的图象过点D，点P是一次函数y=kx+3-3k（k≠0）的图象与该反比例函数的一个公共点．对于一次函数y=kx+3-3k（k≠0），当y随x的增大而增大时，则点P横坐标a的取值范围$\frac{2}{3}$＜a＜3．
7．若二次函数y=x2-（2p+1）x-3p在-1≤x≤1的范围内至少有一个x的值使y≥0成立，则p的取值范围是（　　）
A．p＞2B．p＞0C．p≤2D．0＜p≤2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网