题目内容
15.化简:(1)(2x+1)(2x-1)-(x+1)(3x-2)
(2)$\frac{{x}^{2}-8x+16}{{x}^{2}+2x}$÷(x-2-$\frac{12}{x+2}$)-$\frac{1}{x+4}$.
分析 (1)原式利用平方差公式,以及多项式乘以多项式法则计算,去括号合并即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分后两项计算即可得到结果.
解答 解:(1)原式=4x2-1-3x2+2x-3x+2=x2-x+1;
(2)原式=$\frac{(x-4)^{2}}{x(x+2)}$÷$\frac{(x+4)(x-4)}{x+2}$-$\frac{1}{x+4}$=$\frac{(x-4)^{2}}{x(x+2)}$•$\frac{x+2}{(x+4)(x-4)}$-$\frac{1}{x+4}$=$\frac{x-4}{x(x+4)}$-$\frac{x}{x(x+4)}$=-$\frac{4}{x(x+4)}$.
点评 此题考查了分式的混合运算,多项式乘以多项式,以及平方差公式,熟练掌握公式及法则是解本题的关键.

练习册系列答案
相关题目
5.2017年莒县将以建设莒国古城和开发生态宜居新城为重点,以城带乡、城乡融合,加快推进以人为核心的新型城镇化,在这过程中要完成2.23万套棚户区改造,启动子成范围内15个村和相关单位、居民的搬迁安置,为古城开发打好基础,将2.23万用科学记数法表示为( )
| A. | 22.3×103 | B. | 2.23×104 | C. | 0.223×105 | D. | 2.23×100 |
6. 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
3.2017年5月15日,“一带一路”国际合作高峰论坛在北京雁栖湖国际会议中心举行.据报道,2016年中国与沿线国家贸易总额约为953590000000美元,占中国对外贸易总额的比重达25.7%,将953590000000用科学记数法表示应为( )
| A. | 9.5359×1011 | B. | 95.359×1010 | C. | 0.95359×1012 | D. | 9.5×1011 |
20.怀柔素有“北京后花园”之称,因为有着“一半山水一半城,山凝水重入画屏”的美丽自然景观,吸引着中外游客.2016年1至11月怀柔主要旅游区(点)共接待中外游客约为5870000人次.将5870000用科学记数法表示为( )
| A. | 5.87×105 | B. | 5.87×106 | C. | 0.587×107 | D. | 58.7×105 |
7.宁城县著名AAAA级景区之一---紫蒙湖(原打虎石水库)总面积为400 公顷,总蓄水量为11960 万立方米.数字11960 万立方米用科学记数法表示为( )立方米.
| A. | 1.196×109 | B. | 1.196×108 | C. | 1.196×104 | D. | 11.96×108 |
4.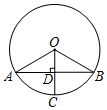 如图,⊙O的半径长3cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
如图,⊙O的半径长3cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
 如图,⊙O的半径长3cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )
如图,⊙O的半径长3cm,点C在⊙O上,弦AB垂直平分OC于点D,则弦AB的长为( )| A. | $\frac{9}{2}$ cm | B. | $\frac{3\sqrt{3}}{2}$cm | C. | 3$\sqrt{3}$cm | D. | $\frac{9}{4}$cm |