题目内容
4．
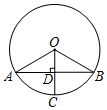如图，⊙O的半径长3cm，点C在⊙O上，弦AB垂直平分OC于点D，则弦AB的长为（ ）| A． | $\frac{9}{2}$ cm | B． | $\frac{3\sqrt{3}}{2}$cm | C． | 3$\sqrt{3}$cm | D． | $\frac{9}{4}$cm |
分析 求出OD，根据勾股定理求出AD，根据垂径定理得出AB=2AD，代入求出即可．
解答 解：∵弦AB垂直平分半径OC，⊙O的半径为3cm，
∴OA=3cm，OD=$\frac{3}{2}$cm，
由勾股定理得：AD=$\sqrt{{3}^{2}-1．{5}^{2}}$=$\frac{3}{2}$$\sqrt{3}$cm，
∵OC过O，OC⊥AB，
∴AB=2AD=3$\sqrt{3}$cm，
故选C．
点评 本题考查了垂径定理和勾股定理的应用，关键是求出AD长和得出AB=2AD．
练习册系列答案
相关题目
14．小张同学去展览馆看展览，该展览馆有2个验票口A、B（可进出），另外还有2个出口C、D（不许进）．小张不从同一个验票口进出的概率是多少（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |
12．在六张卡片上分别写有$\frac{1}{3}$，π，1.5，5，0，$\sqrt{2}$六个数，从中任意抽取一张，卡片上的数为无理数的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{5}{6}$ |
8．有40名大学毕业生在郊区承包了100亩土地，准备种植蔬菜、果树、药材，种植这几种作物每亩所需人数和预测利润见表：
请你设计一个种植方案，既要保证每亩地都种上作物，这40名大学毕业生都有工作，又要保证预测利润的总和最多．
| 作物名称 | 蔬菜 | 果树 | 药材 |
| 每亩地所需的人数（人） | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
| 每亩地的预测利润（元） | 11000 | 7500 | 6000 |