题目内容
 已知:如图,∠ABC=∠ADC,BF平分∠ABC,DE平分∠ADC,且DE∥BF.
已知:如图,∠ABC=∠ADC,BF平分∠ABC,DE平分∠ADC,且DE∥BF.(1)求证:AB∥DC;
(2)AD与BC是否平行?若平行,给出证明;若不平行,说明理由.
考点:平行线的判定与性质
专题:证明题
分析:(1)先根据角平分线的定义得到∠2=
∠ABC,∠CDE=
∠ADC,由于∠ABC=∠ADC,则∠2=∠CDE,根据平行线的判定方法得到DE∥BF,则∠1=∠2,
所以∠1=∠CDE,然后根据同旁内角互补,两直线平行得到AB∥CD;
(2)先根据平行线的性质由AB∥CD得到∠ADC+∠A=180°,由于∠ABC=∠ADC,则∠ABC+∠A=180°,于是根据同旁内角互补,两直线平行可判断AD∥BC.
| 1 |
| 2 |
| 1 |
| 2 |
所以∠1=∠CDE,然后根据同旁内角互补,两直线平行得到AB∥CD;
(2)先根据平行线的性质由AB∥CD得到∠ADC+∠A=180°,由于∠ABC=∠ADC,则∠ABC+∠A=180°,于是根据同旁内角互补,两直线平行可判断AD∥BC.
解答:(1)证明:∵BF平分∠ABC,DE平分∠ADC,
∴∠2=
∠ABC,∠CDE=
∠ADC,
而∠ABC=∠ADC,
∴∠2=∠CDE,
∵DE∥BF,
∴∠1=∠2,
∴∠1=∠2=∠CDE,
∴AB∥CD;
(2)解:AD∥BC.理由如下:
∵AB∥CD,
∴∠ADC+∠A=180°,
而∠ABC=∠ADC,
∴∠ABC+∠A=180°,
∴AD∥BC.
∴∠2=
| 1 |
| 2 |
| 1 |
| 2 |
而∠ABC=∠ADC,
∴∠2=∠CDE,
∵DE∥BF,
∴∠1=∠2,
∴∠1=∠2=∠CDE,
∴AB∥CD;
(2)解:AD∥BC.理由如下:
∵AB∥CD,
∴∠ADC+∠A=180°,
而∠ABC=∠ADC,
∴∠ABC+∠A=180°,
∴AD∥BC.
点评:本题考查了平行线的判定与性质:内错角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,同位角相等;两直线平行,同旁内角互补.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
把分式
分子、分母中a、b都变成原来的2倍,则分式的值变为原分式值的( )
| 2a |
| a+b |
| A、4倍 | B、2倍 |
| C、不变 | D、0.5 倍 |
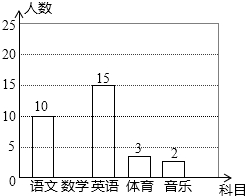 学习委员统计全班50位同学对语文、数学、英语、体育、音乐五个科目最喜欢情况,所得数据用表格与条形图描述如下:
学习委员统计全班50位同学对语文、数学、英语、体育、音乐五个科目最喜欢情况,所得数据用表格与条形图描述如下: 如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.
如图,在?ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C. 如图,在?ABCD中,AC、BD相交于点O,AB⊥AC,AB=AC=2,求BD的长.
如图,在?ABCD中,AC、BD相交于点O,AB⊥AC,AB=AC=2,求BD的长. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=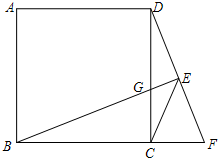 如图,在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.
如图,在正方形ABCD 中,点F是BC延长线上一点,过点B作BE⊥DF于点E,交CD于点G,连接CE.