题目内容
11.已知关于x的方程x2-2(k-3)x+k2-4k-1=0的两实数根之和不小于-6(1)求k的取值范围;
(2)若以方程x2-2(k-3)x+k2-4k-1=0的两个根为横坐标、纵坐标的点恰在反比例函数y=$\frac{m}{x}$ 的图象上,求满足条件的m的取值范围.
分析 (1)若一元二次方程有实数根,则根的判别式△=b2-4ac≥0,建立关于k的不等式,求出k的取值范围.
(2)写出两根之积,两根之积等于m,进而求出m的最小值,再根据k的范围即可求出答案.
解答 解:(1)由题意得△=[-2(k-3)]2-4×(k2-4k-1)≥0
化简得-2k+10≥0,解得k≤5,
∵关于x的方程x2-2(k-3)x+k2-4k-1=0的两实数根之和不小于-6,
∴2(k-3)≥-6,
解得:k≥0,
即k的取值范围是0≤k≤5;
(2)设方程x2-2(k-3)x+k2-4k-1=0的两个根为x1,x2,
根据题意得m=x1x2,
又∵由一元二次方程根与系数的关系得x1x2=k2-4k-1,
那么m=k2-4k-1=(k-2)2-5,所以,当k=2时m取得最小值-5,
∵由(1)知:0≤k≤5,
∴当k=0时,m=(0-2)2-5=-1,当k=5时,m=(5-2)2-5=4,
∴m的取值范围是-5≤m≤4,
∵反比例函数y=$\frac{m}{x}$,
∴m≠0,
综合上述,m的取值范围为-5≤m≤4且m≠0.
点评 本题考查了二次函数的图象和性质,根的判别式等知识点,一元二次方程根的判别式和根与系数的关系,是一个综合性的题目,也是一个难度中等的题目.总结:一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.在等边三角形、平行四边形、矩形、菱形和圆中,既是轴对称图形又是中心对称图形的有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
19.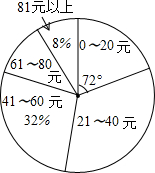 某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?
 某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:
某校初三(1)班的同学踊跃为“希望工程”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但班长不小心把墨水滴在统计表上,部分数据看不清楚.根据图表中现有信息解决下列问题:(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?
| 捐款 | 人数 |
| 0~20元 | |
| 21~40元 | |
| 41~60元 | |
| 61~80元 | 6 |
| 81元以上 | 4 |
6.2017年春学期小红同学四次中考数学测试成绩分别是:103,103,105,105,关于这组数据下列说法错误的是( )
| A. | 平均数是104 | B. | 众数是103 | C. | 中位数是104 | D. | 方差是1 |
16.下列命题中,真命题是( )
| A. | 矩形的对角线相互垂直 | |
| B. | 顺次连结对角线相等的四边形各边中点所得到的四边形是矩形 | |
| C. | 等边三角形既是轴对称图形又是中心对称图形 | |
| D. | 对角线互相垂直平分的四边形是菱形 |
3.随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2=$\frac{1}{2}$x2-11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
| 地铁站 | A | B | C | D | E |
| x(千米) | 8 | 9 | 10 | 11.5 | 13 |
| y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(2)李华骑单车的时间(单位:分钟)也受x的影响,其关系可以用y2=$\frac{1}{2}$x2-11x+78来描述,请问:李华应选择在那一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
20.某种乐器的弦AB长为120cm,点A、B固定在乐器面板上,弦AB之间有一个支撑点C,且点C是AB的黄金分割点(AC>BC),则AC的长为( )
| A. | (120-30$\sqrt{5}$)cm | B. | (160-60$\sqrt{5}$)cm | C. | (60$\sqrt{5}$-120)cm | D. | (60$\sqrt{5}$-6)cm |
 如图,直线y=x+2与反比例函数y=$\frac{k}{x}$的图象在第一象限交于点P,若OP=$\sqrt{10}$,则k的值为3.
如图,直线y=x+2与反比例函数y=$\frac{k}{x}$的图象在第一象限交于点P,若OP=$\sqrt{10}$,则k的值为3.