题目内容
19.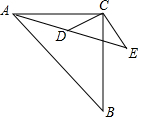 如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.
如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.
分析 过点C作CF⊥DE于F,设DC=x,根据等腰直角三角形的性质可得CF=DF=$\frac{\sqrt{2}}{2}$x,再表示出AF,然后利用勾股定理列方程求解即可.
解答  解:如图,过点C作CF⊥DE于F,设DC=x,
解:如图,过点C作CF⊥DE于F,设DC=x,
∵△ECD是等腰直角三角形,
∴CF=DF=$\frac{\sqrt{2}}{2}$x,
∵AD=2$\sqrt{10}$,
∴AF=AD+DF=AD=2$\sqrt{10}$+$\frac{\sqrt{2}}{2}$x,
在Rt△ACF中,根据勾股定理得,
AF2+CF2=AC2,
即(2$\sqrt{10}$+$\frac{\sqrt{2}}{2}$x)2+($\frac{\sqrt{2}}{2}$x)2=102,
整理得,x2+4$\sqrt{5}$x-60=0,
解得x1=2$\sqrt{5}$,x2=-6$\sqrt{5}$(舍去),
所以,DC的长为2$\sqrt{5}$.
点评 本题考查了等腰直角三角形的性质,勾股定理,一元二次方程的解法,作辅助线,构造出直角三角形并利用勾股定理列出方程是解题的关键.

练习册系列答案
相关题目
9.下列各组数据中,平均数和中位数相等的是( )
| A. | 1,2,3,4,5 | B. | 1,3,4,5,6 | C. | 1,2,4,5,6 | D. | 1,2,3,5,6 |

 在平面直角坐标系中,点A(-2a,a-1)在x轴上,将点A向右平移5个单位长度,向上平移m(m>2)个单位长度,得到点B,直线l是平行于x轴,纵坐标都是1的直线,点C与点B关于直线l轴对称.
在平面直角坐标系中,点A(-2a,a-1)在x轴上,将点A向右平移5个单位长度,向上平移m(m>2)个单位长度,得到点B,直线l是平行于x轴,纵坐标都是1的直线,点C与点B关于直线l轴对称.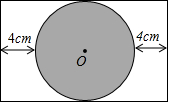 电视显示屏的屏保图是阴影部分的圆O(矩形中最大的圆),屏保图在显示屏(矩形)中的位置如图,若⊙O的面积为400πcm2,求矩形显示屏的长.
电视显示屏的屏保图是阴影部分的圆O(矩形中最大的圆),屏保图在显示屏(矩形)中的位置如图,若⊙O的面积为400πcm2,求矩形显示屏的长. 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.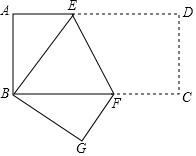 如图,矩形ABCD中,AB=6,CB=18,若将矩形折叠使B与D重合,则折痕EF的长为2$\sqrt{10}$.
如图,矩形ABCD中,AB=6,CB=18,若将矩形折叠使B与D重合,则折痕EF的长为2$\sqrt{10}$.